IDEE PER UNA SCIENZA UMANA E NATURALE
Gli infiniti Universi e la coda alle poste

Le due cose sembrerebbero non avere niente a che fare l’una con l’altra e invece un punto in comune c’è ed è John David Barrow, classe 1952, professore di matematica all'Università di Cambridge, uno dei grandi della cosmologica. Barrow ha tenuto l’anno scorso una lectio magistralis intitolata “Universi” al festival della scienza di Genova, descrivendo Universi in espansione, in rotazione, caotici, in accelerazione e i “Multiversi”, veri e propri Universi paralleli coesistenti e alternativi al nostro. Qualcosa che Giordano Bruno aveva già intuito più di quattrocento anni fa: “Or ecco, vi porgo la mia contemplazione circa l'infinito, universo e mondi innumerabili” (De l'Infinito Universo et Mondi). Sfortunatamente, questi mondi sarebbero così lontani da essere irraggiungibili anche con le più ottimistiche ipotesi sui progressi della tecnologia e dunque il concetto di Multiverso sembra destinato a rimanere per sempre nel regno della metafisica.
In campo cosmologico di Barrow è nota soprattutto la teoria del “principio antropico”, che ha aperto un dibattito nel mondo scientifico con proseliti e denigratori. Il principio antropico si basa su quella che sembrerebbe a prima vista un'ovvietà: l'Universo e le sue leggi non possono essere incompatibili con la nostra esistenza. Se, infatti, non esistessero straordinarie coincidenze nelle leggi fisiche e nei valori delle costanti fondamentali della natura, la biochimica, la vita e la vita intelligente non sarebbero possibili. Non sarebbero possibili neppure gli oggetti astronomici comuni e la materia ordinaria.
Barrow è autore di centinaia di pubblicazioni scientifiche di cosmologia e astrofisica, ma rimane tuttavia, in primis, un matematico. Ha anche scritto alcuni libri divulgativi tra i quali “100 cose essenziali che non sapevate di non sapere”, sottotitolo “i meccanismi segreti del mondo che ci circonda” (Oscar Mondadori 2011). Il libro risponde con un linguaggio accessibile ai più, ma in modo rigoroso, a un numero di quesiti derivati dalla vita di tutti i giorni. Qualche esempio:
Perché quando siamo in coda la fila accanto è sempre più veloce della nostra?
E’ possibile prevedere i record?
E’ possibile che una scimmia battendo dei tasti a caso possa riuscire a riprodurre un’opera di Shakespeare?
Che la matematica sia importante lo dimostra quanto fosse tenuta in considerazione dai Greci. In particolare Platone, nella Repubblica, tratteggia un ambizioso piano educativo per creare un’utopistica figura di governatore con una formazione precoce nell’infanzia che prevedeva non meno di dieci anni di studi di matematica. Egli spiega che i potenziali uomini politici non devono amare governare, altrimenti la loro rivalità sfocerà in contesa, ma conoscere i metodi per la migliore amministrazione dello Stato. Anche George Washington riteneva la conoscenza della matematica e della filosofia utile per i futuri politicanti, poiché queste abituano la mente al metodo e alla correttezza di ragionamento. Nell’attuale atmosfera preelettorale Italiana questi consigli fanno un po’ sorridere!
Dal libro di Barrow ho selezionato tre quesiti a mio avviso tra i più interessanti. Forse le domande potranno sembrare banali, ma le risposte non lo sono assolutamente!
Perché l’altra fila è sempre più veloce?
Sembrerebbe l’enunciato di una delle così dette “leggi di Murphy” o forse una dimostrazione della paranoia umana. In realtà alla base c’è la poca simpatia degli esseri umani per la statistica: noi, infatti, siamo “in media” (questo è il punto!) nella fila più lenta semplicemente perché le file lente sono costituite da più persone, ed è più probabile trovarsi in una di queste piuttosto che in una con poche persone (che si muove più velocemente). E’ una specie di selezione naturale. Barrow estende il ragionamento notando che lo stesso vale se osserviamo l’Universo tenendo presente il principio copernicano (che afferma che la Terra non è in una posizione centrale o di particolare privilegio). In realtà anche se il principio vale in termini generali, sarebbe un errore credere di non essere speciali in senso particolare: la vita è possibile solo in quei luoghi in cui esistono condizioni speciali. E’ più probabile trovarla dove ci sono stelle e pianeti, dove cioè l’abbondanza di materia è superiore alla media. Il richiamo al principio antropico è evidente.
E’ un record?
Sembrerebbe che i record (non parliamo di quelli sportivi, ma di quelli ad esempio che si riferiscono alle precipitazioni o alle temperature in un certo luogo in un certo intervallo di tempo) siano eventi indipendenti tra loro. Prendiamo ad esempio le registrazioni annuali delle piogge in un certo luogo e cominciamo a catalogare i record. Il primo anno è da record ovviamente, mentre nel secondo avremo una probabilità 1 a 2 di battere il record (ma anche di non batterlo). Nei primi 2 anni ci aspettiamo quindi un numero di record uguale a 1 + 1/2 (cioè 1,5). Continuando il ragionamento, nel terzo anno il numero di record sarà 1 + 1/2 + 1/3 (cioè 1,833) e così via per n anni. Questa è la famosa “serie armonica”, che ha la caratteristica di crescere molto lentamente con l’aumentare dei termini (per n= 1.000.000 vale 14,39).
Tornando alle piogge, se consideriamo ad esempio gli ultimi 256 anni, potremo prevedere di trovare solo 6,12 (valore della serie per n=256) record, diciamo circa 6 record di forti (o deboli) precipitazioni. Osservando i record delle precipitazioni presso la stazione meteorologica di Kew Gardens a Londra il valore è proprio questo!
Barrow fa notare che una deviazione del numero di record dalla serie armonica indica, di converso, una non indipendenza degli eventi. Per esempio i recenti eventi climatici legati al così detto “riscaldamento globale” andrebbero analizzati per verificare se sia iniziata una tendenza sistematica non casuale.
Le scimmie e Shakespeare
L’ipotesi originale è del matematico francese Emile Borel (1781-1956), il quale si chiese se fosse possibile che delle scimmie battendo sui tasti di una macchina da scrivere potessero riprodurre tutti i libri della Bibliothèque Nationale. Per provare quest’affermazione, il sito Internet Monkey Shakespeare Simulator Project tempo fa simulò a computer il battere casuale dei tasti e confrontando il risultato ottenuto, in ambito più anglosassone, con le Opere Complete di Shakespeare.
Il progetto è iniziato il 1° luglio 2003 con 100 scimmie “virtuali” ed è durato fino al 2007. Si è passati da una sequenza di 19 caratteri, che è stata per parecchio tempo la più lunga, alla sequenza più lunga mai prodotta di 24 caratteri nel 2005, dopo 2.737.850 milioni di miliardi di miliardi di “anni scimmia”, corrispondente a una frase dell’Enrico IV. Basta solo aspettare dice Barrow!
Che morale possiamo trarre da questo gioco? Possiamo dedurre che un evento che abbia bassissime probabilità di accadere, può invece accadere quando si consideri un intervallo di tempo estremamente lungo o un numero di tentativi estremamente alto. Ad esempio le probabilità di fare 14 al totocalcio sono 1/314 = 1/4.782.969 (in realtà è un po’ meglio, dato che le colonne con molti 2 sono altamente improbabili e non andrebbero contate). Una probabilità su quasi cinque milioni sembra poco, ma con milioni di giocatori un 14 uscirebbe abbastanza frequentemente (su 1.333.896 di colonne giocate nell’ultimo concorso i 14 sono stati 28).
La magia dei numeri
Per terminare qualche “chicca” sui numeri, che fa pensare che qualcosa di magico esista davvero nella matematica.
Consideriamo il numero di giorni che ci sono in un anno: 365. E’ facile verificare che 365 è uguale alla somma di tre quadrati consecutivi: 365 = 102 + 112 + 122. E’ anche la somma dei due quadrati seguenti: 365 = 132 + 142. Il numero dei giorni di un mese lunare, 28, è uguale alla somma di tutti i suoi divisori: 28 = 1 + 2 + 4 + 7 + 14. Numeri così vengono chiamano “numeri perfetti”. A oggi si conoscono 47 numeri perfetti, il più grande dei quali ha 25.956.377 cifre! Si noti che 28 è anche uguale alla somma dei primi due numeri dispari: 28 = 13 +33. Un numero largamente usato nel sistema decimale, 100, è la somma dei cubi dei primi quattro numeri: 100 = 13 + 23 + 33 + 43.
I pitagorici, cioè Pitagora e il gruppo di discepoli raccolti intorno a lui presso Crotone, avevano uno stile di vita che si basava sul vegetarianismo, su una forte credenza nella metempsicosi e sulla misteriosa proibizione di mangiare le fave. Essi adoravano il numero cinque, che rappresenta la somma del primo numero pari con il primo numero dispari (il numero 1 non era considerato un numero dai greci). Uno dei simboli della scuola pitagorica era, infatti, il pentagono stellato che si disegna tracciando tutte le diagonali possibili di un pentagono regolare fino a ottenere una stella a cinque punte.
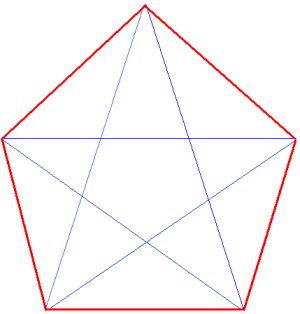
Tra l’altro il rapporto di qualunque diagonale di un pentagono con il suo lato si chiama “rapporto aureo” (o “sezione aurea”), tanto famoso sia in geometria sia in arte e considerato misterioso (se non addirittura divino) dai greci. Per inciso, nel 1611 il grande Keplero scoperse che esisteva una relazione tra il numero aureo e la serie di Fibonacci (di cui lo stesso Fibonacci non era a conoscenza). La serie di Fibonacci è 1, 2, 3, 5, 8, ecc, in cui ogni termine è la somma dei due precedenti.
Nel Timeo, Platone tentò di spiegare la struttura della materia utilizzando i cinque solidi regolari (detti, appunto, “solidi platonici”), e cioè il tetraedro, il cubo (o esaedro), l’ottaedro, il dodecaedro e l’icosaedro (che ha 20 facce). Questi solidi sono gli unici in cui tutte le facce sono uguali e sono poligoni regolari i cui vertici poggiano tutti su una sfera. Platone associò i quattro elementi cosmici primari a quattro solidi regolari: la terra al cubo, il fuoco al tetraedro, l’aria all’ottaedro e l’acqua all’icosaedro. Al dodecaedro Platone associò l’Universo nella sua interezza.
Non stupisce che Pitagora affermasse con enfasi che “Tutto è numero”!
Fonte: Logos, Anno XXII – I – 2013 logostrimestrale.blogspot.it - www.lombardiainrete.it/12/Varie/Logos/