




Avanti: ProbabilitÓ di errore
Su: ProbabilitÓ di Errore nelle Trasmissioni Numeriche
Indietro: ProbabilitÓ di Errore nelle Trasmissioni Numeriche
Indice
Indice analitico
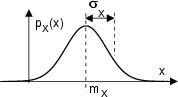
Una variabile aleatoria gaussiana x Ŕ descritta da una densitÓ di probabilitÓ
di espressione
il cui andamento Ŕ mostrato in figura, dove Ŕ posto in evidenza come mx
e
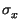 (media e deviazione standard) siano in relazione la prima
con la centratura orizzontale, e la seconda con la dispersione della curva attorno
alla media. Oltre che da un punto di vista grafico, i primi due momenti della
v.a. descrivono completamente la densitÓ anche dal punto di vista analitico;
pertanto, la stima di questi (ad esempio a partire da un buon numero di realizzazioni5.27) Ŕ sufficiente per descrivere completamente il fenomeno aleatorio.
(media e deviazione standard) siano in relazione la prima
con la centratura orizzontale, e la seconda con la dispersione della curva attorno
alla media. Oltre che da un punto di vista grafico, i primi due momenti della
v.a. descrivono completamente la densitÓ anche dal punto di vista analitico;
pertanto, la stima di questi (ad esempio a partire da un buon numero di realizzazioni5.27) Ŕ sufficiente per descrivere completamente il fenomeno aleatorio.
La v.a. gaussiana descrive bene una moltitudine di fenomeni naturali, ed Ŕ dimostrabile
analiticamente che la sua densitÓ Ŕ caratteristica di grandezze generate dalla
somma di un numero molto elevato di cause aleatorie, tutte con la medesima DDP5.28 (teorema del limite centrale).
La funzione di distribuzione di questa v.a. non Ŕ calcolabile in forma chiusa;
fortunatamente per˛, stante la necessitÓ di conoscere la probabilitÓ di eventi
gaussiani, sono disponibili tabelle e grafici, che riportano il valore numerico
dell'integrale che definisce tali valori di probabilitÓ.
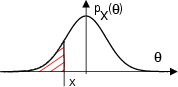
Per renderci conto della situazione, proviamo a calcolare la probabilitÓ che
X non superi un certo valore x, pari per definizione alla funzione
di distribuzione, e rappresentata dall'area tratteggiata in figura (per semplicitÓ
ci riferiamo ad una gaussiana a media nulla):
FX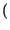 x
x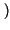 = Pr
= Pr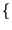 X
X 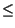 x
x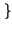 =
= 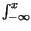 pX
pX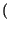

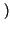 d
d = 1 -
= 1 - 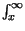
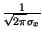 e-
e- 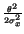 d
d .
Effettuiamo ora un cambio di variabile, ponendo
.
Effettuiamo ora un cambio di variabile, ponendo
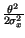 =
= 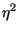 ,
per cui in corrispondenza di
,
per cui in corrispondenza di  = x si ha
= x si ha
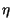 =
= 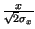 ,
e risulta
d
,
e risulta
d =
= 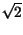
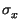 d
d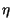 . Con queste posizioni, possiamo
riscrivere
. Con queste posizioni, possiamo
riscrivere
Cosa Ŕ successo ? Semplicemente, abbiamo espresso l'integrale (irrisolvibile
in forma chiusa) nei termini della ``funzione''
erfc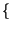 .
.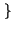 ,
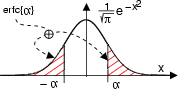
che rappresenta la probabilitÓ che una v.a. gaussiana a media nulla e varianza
,
che rappresenta la probabilitÓ che una v.a. gaussiana a media nulla e varianza
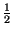 superi (in valore assoluto) il valore dato come argomento,
come mostrato in figura, e pari a
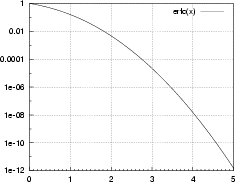
I valori di erfc in funzione del suo argomento sono reperibili sia in
forma di tabelle numeriche, che in forma di diagrammi quotati5.29.
superi (in valore assoluto) il valore dato come argomento,
come mostrato in figura, e pari a
I valori di erfc in funzione del suo argomento sono reperibili sia in
forma di tabelle numeriche, che in forma di diagrammi quotati5.29.
In linea generale quindi, volendo calcolare la probabilitÓ che una v.a. gaussiana
X, con media mx e varianza
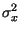 , superi in
ampiezza un determinato valore
, superi in
ampiezza un determinato valore 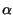 , l'unica strada percorribile Ŕ
quella di utilizzare la funzione erfc, avendo cura di porre come argomento
il valore di
, l'unica strada percorribile Ŕ
quella di utilizzare la funzione erfc, avendo cura di porre come argomento
il valore di 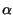 debitamente scalato, per ricondursi ad una gaussiana
a media nulla e varianza
debitamente scalato, per ricondursi ad una gaussiana
a media nulla e varianza
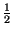 :
:





Avanti: ProbabilitÓ di errore
Su: ProbabilitÓ di Errore nelle Trasmissioni Numeriche
Indietro: ProbabilitÓ di Errore nelle Trasmissioni Numeriche
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
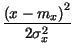
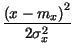
![]() x
x![]() = Pr
= Pr![]() X
X ![]() x
x![]() =
= ![]() pX
pX![]()
![]()
![]() d
d![]() = 1 -
= 1 - ![]()
![]() e-
e- ![]() d
d![]() .
Effettuiamo ora un cambio di variabile, ponendo
.
Effettuiamo ora un cambio di variabile, ponendo
![]() =
= ![]() ,
per cui in corrispondenza di
,
per cui in corrispondenza di ![]() = x si ha
= x si ha
![]() =
= ![]() ,
e risulta
d
,
e risulta
d![]() =
= ![]()
![]() d
d![]() . Con queste posizioni, possiamo
riscrivere
. Con queste posizioni, possiamo
riscrivere
![]() , superi in
ampiezza un determinato valore
, superi in
ampiezza un determinato valore ![]() , l'unica strada percorribile Ŕ
quella di utilizzare la funzione erfc, avendo cura di porre come argomento
il valore di
, l'unica strada percorribile Ŕ
quella di utilizzare la funzione erfc, avendo cura di porre come argomento
il valore di ![]() debitamente scalato, per ricondursi ad una gaussiana
a media nulla e varianza
debitamente scalato, per ricondursi ad una gaussiana
a media nulla e varianza
![]() :
: