Dipendenza di Pe da Eb/No

L'SNR che appare nell'argomento dell'erfc in realtà non è una variabile indipendente del collegamento, in quanto la potenza di rumore $\mathcal {P}$_N = N₀B_N, da cui SNR dipende, a sua volta è funzione dalla banda del filtro di ricezione, che come abbiamo visto è posta pari al massima frequenza presente in r$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, e (nel consueto caso di g$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ a coseno rialzato) pari a

B_N = $${\frac{f_{L}}{2}}$$$$\left(\vphantom{ 1+\gamma }\right.$$1 + $$\gamma$$ $$\left.\vphantom{ 1+\gamma }\right)$$ = $${\frac{f_{b}}{2\log _{2}L}}$$$$\left(\vphantom{ 1+\gamma }\right.$$1 + $$\gamma$$ $$\left.\vphantom{ 1+\gamma }\right)$$

dipendendo quindi anch'essa da L e $\gamma$, oltre che dalla f_b. Pertanto, al variare di L e $\gamma$, varia anche SNR, complicando un poco il ragionamento esposto al termine della precedente sezione.

Allo scopo di mantenere separati tra loro i diversi elementi che determinano la probabilità di errore, e di porre nella giusta evidenza i parametri di sistema f_b ed N₀, esprimiamo le potenze $\mathcal {P}$_N e $\mathcal {P}$_R in funzione di T_b = 1/f_b:

$$\mathcal {P}$$_N = N₀B_N = $${\frac{N_{0}\left( 1+\gamma \right) }{T_{b}2\log _{2}L}}$$    e    $$\mathcal {P}$$_R = $${\frac{E_{b}}{T_{b}}}$$

in modo da ottenere

SNR = $${\frac{\mathcal{P}_{R}}{\mathcal{P}_{N}}}$$ = $${\frac{E_{b}}{T_{b}}}$$$${\frac{T_{b}2\log _{2}L}{N_{0}\left( 1+\gamma \right) }}$$ = $${\frac{E_{b}}{N_{0}}}$$$${\frac{2\log _{2}L}{\left( 1+\gamma \right) }}$$

La grandezza E_b rappresenta l'energia per bit^5.36 e la sua definizione

E_b = $$\mathcal {P}$$_RT_b = $${\frac{\mathcal{P}_{R}}{f_{b}}}$$

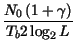mostra come essa riassume in sè i parametri di sistema potenza di segnale e velocità binaria, mentre invece non dipende dai parametri di trasmissione L e $\gamma$. Anche N₀, inoltre, costituisce un parametro di sistema, rappresentando una grandezza su cui non è possibile intervenire.

Adottando le posizioni esposte, il quadrato dell'argomento dell'erfc è espresso ora come:

y² = $${\textstyle\frac{3}{2}}$$SNR$${\frac{1}{\left( L^{2}-1\right) \left( 1-\frac{\gamma }{4}\right) }}$$ = $${\frac{E_{b}}{N_{0}}}$$$${\frac{3\log _{2}L}{\left( L^{2}-1\right) \left( 1+\gamma \right) \left( 1-\frac{\gamma }{4}\right) }}$$

Come la precedente, anche questa relazione può ben essere utilizzata per valutare il valore dell'argomento dell'erfc ed usare quindi le curve per determinare la probabilità di errore. In particolare, notiamo che per L = 2 e $\gamma$ = 0 si ottiene: P_e = ${\frac{1}{2}}$erfc$\left\{\vphantom{ \sqrt{\frac{E_{b}}{N_{0}}}}\right.$$\sqrt{\frac{E_{b}}{N_{0}}}$ $\left.\vphantom{ \sqrt{\frac{E_{b}}{N_{0}}}}\right\}$, che assume il ruolo di valore di riferimento: infatti, il termine sotto radice contraddistingue le condizioni operative della trasmissione (racchiudendo potenza ricevuta, frequenza binaria e livello di rumore). Le scelte progettuali (roll-off e numero di livelli) diverse da L = 2 e $\gamma$ = 0 determinano immancabilmente un peggioramento della P_e, ma vengono intraprese per soddisfare esigenze di risparmio di banda (aumentando L)^5.37, e per ridurre i termini di interferenza intersimbolica (aumentando $\gamma$). In particolare, la compensazione (con f_b fissa) del peggioramento di P_e dovuto ad uno (o ad entrambi) questi fattori, può avvenire solamente grazie ad un aumento di E_b, ovvero un aumento della potenza trasmessa: tale circostanza è nota come compromesso banda-potenza^5.38.

Due domande riassuntive:

1) Perché P_e peggiora se aumento i livelli ?

2) Perché P_e peggiora se aumento $\gamma$ ?

Risposte:

1) Perché a parità di $\mathcal {P}$_R gli intervalli di decisione sono più ravvicinati, e le ``code'' della gaussiana sottendono un'area maggiore.

2) Perché occorre aumentare la banda del filtro di ricezione e dunque far entrare più rumore. D'altra parte questo peggioramento è compensato dalla riduzione dell'ISI.