




Avanti: Esempi
Su: DensitÓ Spettrale
Indietro: DensitÓ Spettrale
Indice
Indice analitico
Lo spettro di densitÓ di potenza
 x
x f
f (o di energia
(o di energia
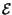 x
x f
f ) di
x
) di
x t
t Ŕ uguale alla trasformata di Fourier della sua funzione di autocorrelazione
Ŕ uguale alla trasformata di Fourier della sua funzione di autocorrelazione
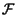
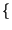
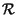 x
x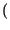

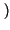
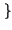 .
.
La dimostrazione del teorema Ŕ straordinariamente semplice, e per segnali di
energia si scrive
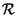 x x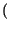 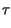 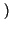 |
= |
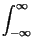 x* x* t t x x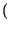 t + t + 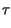 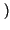 dt = dt = 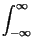 X* X*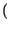 f f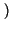 X X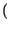 f f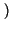 ej2 ej2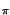 f f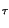 df = df = |
|
| |
= |
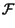 -1 -1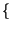 X* X*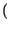 f f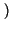 X X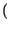 f f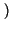 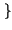 = = 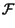 -1 -1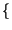 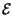 x x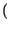 f f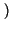 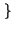 |
|
in cui abbiamo prima applicato il teorema di Parseval, poi la proprietÓ di traslazione
nel tempo, e quindi espresso
X* f
f X
X f
f come
come
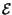 x
x f
f .
.
Per segnali di potenza la dimostrazione Ŕ del tutto simile, e valida anche per
realizzazioni di processi. In particolare, se il processo Ŕ ergodico, la media
di insieme
mX1X2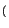 1, 1
1, 1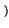 risulta uguale alla media
temporale calcolata per ogni realizzazione del processo, e pertanto lo spettro
di densitÓ di potenza di un processo si ottiene trasformando la funzione di
autocorrelazione calcolata come media di insieme, oppure trasformando quella
calcolata come media temporale per una delle sue realizzazioni.
risulta uguale alla media
temporale calcolata per ogni realizzazione del processo, e pertanto lo spettro
di densitÓ di potenza di un processo si ottiene trasformando la funzione di
autocorrelazione calcolata come media di insieme, oppure trasformando quella
calcolata come media temporale per una delle sue realizzazioni.
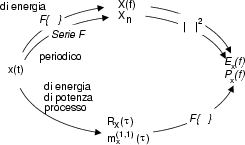
Pertanto, grazie al Teorema di Wiener, Ŕ possibile ottenere
 x
x f
f anche per processi, oppure fare ``la prova del nove'' per segnali di energia
o periodici.
anche per processi, oppure fare ``la prova del nove'' per segnali di energia
o periodici.





Avanti: Esempi
Su: DensitÓ Spettrale
Indietro: DensitÓ Spettrale
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
x
f
(o di energia
x
f
) di x
t
Ŕ uguale alla trasformata di Fourier della sua funzione di autocorrelazione
x

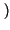
.
![]() x
x![]() f
f![]() anche per processi, oppure fare ``la prova del nove'' per segnali di energia
o periodici.
anche per processi, oppure fare ``la prova del nove'' per segnali di energia
o periodici.