




Avanti: Segnali periodici
Su: Filtraggio di segnali e processi
Indietro: Filtraggio di segnali e processi
Indice
Indice analitico
Sappiamo che per il teorema di Parseval risulta
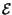 y
y f
f = Y
= Y f
f Y*
Y* f
f ;
dato che
Y
;
dato che
Y f
f = X
= X f
f H
H f
f , allora
, allora
A questo punto, eseguendo l'antitrasformata di Fourier di ambo i membri, si
ottiene:
Il risultato ottenuto è posto in evidenza perché è valido anche per i due casi
successivi di segnale periodico e di processo, e mostra come l'autocorrelazione
dell'uscita di un filtro è pari alla convoluzione tra l'autocorrelazione dell'ingresso
e quella della risposta impulsiva.
A corollario di quanto esposto, sussistono i seguenti integrali7.14, equivalenti ai fini del calcolo dell'energia totale:
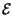 y y |
= |
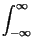 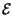 y y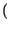 f f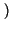 df = df = 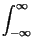 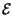 x x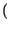 f f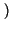 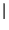 H H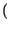 f f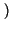 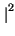 df = df = 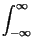 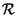 x x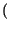 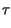 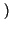 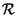 H H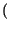 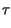 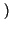 d d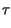 = = |
|
| |
= |
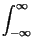 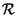 x x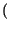 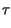 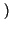 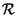 H* H*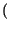 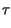 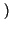 d d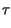 = = 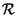 y y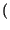 0 0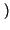 |
|
Pertanto è possibile utilizzare tutte queste come relazioni di equivalenza,
quando si ha necessità di determinare una grandezza a partire da altre note.





Avanti: Segnali periodici
Su: Filtraggio di segnali e processi
Indietro: Filtraggio di segnali e processi
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() y
y![]() f
f![]() = Y
= Y![]() f
f![]() Y*
Y*![]() f
f![]() ;
dato che
Y
;
dato che
Y![]() f
f![]() = X
= X![]() f
f![]() H
H![]() f
f![]() , allora
, allora