




Avanti: Somma
Su: UnitÓ di elaborazione
Indietro: UnitÓ di elaborazione
Indice
Indice analitico
Nel caso in cui un fattore sia un processo, e l'altro
un segnale certo, il risultato (in generale) Ŕ un processo non stazionario.
Infatti ora le medie d'insieme dipendono, istante per istante, dal valore che
il segnale certo assume in quell'istante (tranne il caso in cui sia una costante)7.17.
Se uno dei due fattori (ad es
y t
t ) Ŕ una costante,
z
) Ŕ una costante,
z t
t Ŕ un processo della stessa natura di
x
Ŕ un processo della stessa natura di
x t
t , con media
mz = mx . y,
potenza
, con media
mz = mx . y,
potenza
 z =
z =  x . y2, e autocorrelazione
x . y2, e autocorrelazione
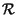 z
z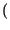

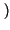 =
= 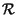 x
x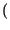

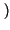 . y2.
. y2.
Se i fattori
x t
t ed
y
ed
y t
t sono processi
statisticamente indipendenti, stazionari e congiuntamente7.18 ergodici, si ottiene:
sono processi
statisticamente indipendenti, stazionari e congiuntamente7.18 ergodici, si ottiene:
- Valor medio
-
-
| mz |
= |
E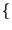 z z t t 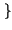 = E = E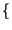 x x t t y y t t 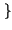 = E = E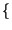 x x t t 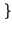 E E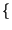 y y t t 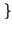 = = |
| |
= |
mx . my |
-
- Potenza totale
-
-
 z z |
= |
E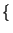 z2 z2 t t 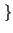 = E = E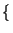 x2 x2 t t y2 y2 t t 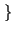 = E = E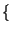 x2 x2 t t 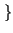 E E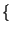 y2 y2 t t 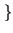 |
| |
= |
 x . x .  y y |
-
- Varianza
-
-
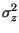 |
= |
E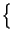 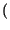 z z t t - mz - mz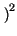 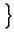 = =  z - z - 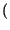 mz mz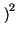 = = |
| |
= |
 x . x .  y - y - 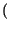 mx . my mx . my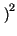 |
-
- Funzione di autocorrelazione
-
-
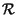 z z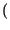  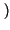 |
= |
E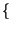 z z t t z z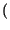 t + t +  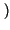 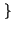 = E = E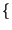 x x t t y y t t x x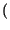 t + t +  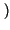 y y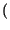 t + t +  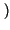 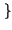 = = |
| |
= |
E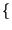 x x t t x x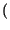 t + t +  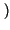 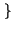 E E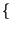 y y t t y y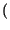 t + t +  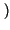 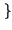 = = 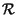 x x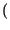  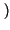 . . 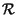 y y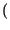  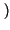 |
-
In particolare, notiamo che l'incorrelazione di uno dei due processi, per un
certo valore di  , provoca l'incorrelazione del prodotto.
, provoca l'incorrelazione del prodotto.
- Spettro di densitÓ di potenza
-
-
-
ossia Ŕ pari alla convoluzione tra le densitÓ spettrali dei fattori. Notiamo
quindi che la densitÓ di potenza del prodotto presenta una occupazione di banda
maggiore di quella dei singoli fattori.
- DensitÓ di probabilitÓ
- Si calcola con le regole per il cambiamento di variabile,
che non abbiamo trattato. Nel caso in cui i due processi siano statisticamente
indipendenti, il risultato Ŕ
-
pZ
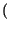 z
z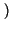 =
= 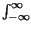 pX
pX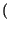

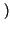 pY
pY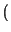
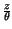
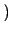
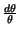 .
.
-
In Appendice (pag. ![[*]](cross_ref_motif.gif) ), troviamo l'applicazione di questi
risultati al calcolo della densitÓ di potenza dell'onda PAM.
), troviamo l'applicazione di questi
risultati al calcolo della densitÓ di potenza dell'onda PAM.





Avanti: Somma
Su: UnitÓ di elaborazione
Indietro: UnitÓ di elaborazione
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() t
t![]() ) Ŕ una costante,
z
) Ŕ una costante,
z![]() t
t![]() Ŕ un processo della stessa natura di
x
Ŕ un processo della stessa natura di
x![]() t
t![]() , con media
mz = mx . y,
potenza
, con media
mz = mx . y,
potenza
![]() z =
z = ![]() x . y2, e autocorrelazione
x . y2, e autocorrelazione
![]() z
z![]()
![]()
![]() =
= ![]() x
x![]()
![]()
![]() . y2.
. y2.
![]() t
t![]() ed
y
ed
y![]() t
t![]() sono processi
statisticamente indipendenti, stazionari e congiuntamente7.18 ergodici, si ottiene:
sono processi
statisticamente indipendenti, stazionari e congiuntamente7.18 ergodici, si ottiene:
![[*]](cross_ref_motif.gif) ), troviamo l'applicazione di questi
risultati al calcolo della densitÓ di potenza dell'onda PAM.
), troviamo l'applicazione di questi
risultati al calcolo della densitÓ di potenza dell'onda PAM.