Avanti: Filtri Analogici
Su: Filtri Digitali
Indietro: Stima della autocorrelazione di un processo
Indice
Indice analitico
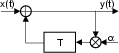
Lo schema riportato a fianco è un filtro di tipo ricorsivo in cui l'uscita
dipende dalle precedenti uscite. La sua risposta impulsiva ha durata
infinita ed è pari a
La sua funzione di trasferimento risulta pari a
H f
f =
= 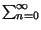
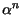 e-j2
e-j2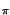 fnT
e, ricordando la formula dello sviluppo in serie geometrica
fnT
e, ricordando la formula dello sviluppo in serie geometrica
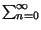
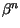 =
= 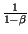 ,
si può scrivere
,
si può scrivere
Notiamo subito che il filtro è stabile purchè
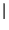
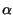
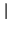 < 1,
altrimenti si ha una uscita anche senza ingresso, ovvero uscita infinita con
ingresso limitato. Per ciò che riguarda
< 1,
altrimenti si ha una uscita anche senza ingresso, ovvero uscita infinita con
ingresso limitato. Per ciò che riguarda
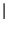 H
H f
f
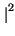 ,
otteniamo
,
otteniamo
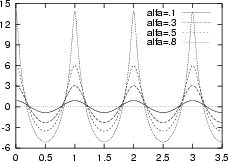
Il grafico a lato rappresenta
10log10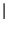 H
H f
f
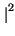 ,
con T = 1 e diversi valori di
,
con T = 1 e diversi valori di 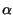 . Osserviamo infine che il
caso
. Osserviamo infine che il
caso 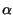 = 1 corrisponde ad avere un integratore perfetto che, ad esempio,
produce una rampa in uscita, se in ingresso c'è un gradino.
= 1 corrisponde ad avere un integratore perfetto che, ad esempio,
produce una rampa in uscita, se in ingresso c'è un gradino.





Avanti: Filtri Analogici
Su: Filtri Digitali
Indietro: Stima della autocorrelazione di un processo
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01

![]() f
f![]() =
= ![]()
![]() e-j2
e-j2![]() fnT
e, ricordando la formula dello sviluppo in serie geometrica
fnT
e, ricordando la formula dello sviluppo in serie geometrica
![]()
![]() =
= ![]() ,
si può scrivere
,
si può scrivere