Avanti: Formule di Eulero
Su: Prerequisiti trigonometrici
Indietro: Prerequisiti trigonometrici
Indice
Indice analitico
Un numero complesso
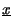 è costituito da una coppia di valori
numerici a e b che ne rappresentano la parte reale e quella immaginaria:
è costituito da una coppia di valori
numerici a e b che ne rappresentano la parte reale e quella immaginaria:
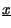
=
a +
jb
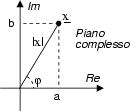
E' spesso utile ricorrere ad una rappresentazione di
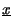 nel
piano complesso, che mette in luce l'espressione alternativa di
nel
piano complesso, che mette in luce l'espressione alternativa di
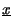 nei termini di modulo
nei termini di modulo
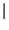 x
x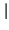 e fase
e fase 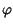 :
Queste due quantità si ottengono dalle parti reale ed immaginaria, mediante
le relazioni
mentre le relazioni inverse risultano
Per ogni numero complesso
:
Queste due quantità si ottengono dalle parti reale ed immaginaria, mediante
le relazioni
mentre le relazioni inverse risultano
Per ogni numero complesso
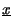 , è definito il suo coniugato
, è definito il suo coniugato
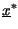 come quel numero complesso con uguale parte reale,
e parte immaginaria di segno opposto, ovvero uguale modulo, e fase cambiata
di segno:
come quel numero complesso con uguale parte reale,
e parte immaginaria di segno opposto, ovvero uguale modulo, e fase cambiata
di segno:
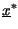 = a - jb =
= a - jb =  x
x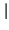 e-j
e-j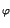 .
.
alef@infocom.uniroma1.it
2001-06-01