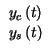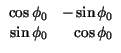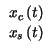Nel caso in cui un segnale modulato
x![]() t
t![]() presenti una occupazione
di frequenza molto piccola rispetto alla frequenza portate, si assume spesso
che
H
presenti una occupazione
di frequenza molto piccola rispetto alla frequenza portate, si assume spesso
che
H![]() f
f![]() nella banda di segnale non vari di molto, ossia
presenti sia modulo che fase pressoché costanti e pari al valore assunto per
f = f0, ossia
H
nella banda di segnale non vari di molto, ossia
presenti sia modulo che fase pressoché costanti e pari al valore assunto per
f = f0, ossia
H![]() f
f![]()
![]() H
H![]() f0
f0![]() = G0ej
= G0ej![]() .
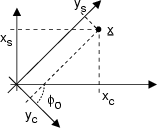
Questa approssimazione permette di trascurare l'effetto delle distorsioni lineari,
che in questo caso equivalgono ad una semplice rotazione degli assi dell'inviluppo
complesso, reversibile scegliendo opportunamente la fase della portante di demodulazione.
.
Questa approssimazione permette di trascurare l'effetto delle distorsioni lineari,
che in questo caso equivalgono ad una semplice rotazione degli assi dell'inviluppo
complesso, reversibile scegliendo opportunamente la fase della portante di demodulazione.
Nelle ipotesi poste, risulta infatti
![]()
![]() f
f![]() = 2H+
= 2H+![]() f + f0
f + f0![]() = 2G0ej
= 2G0ej![]() e quindi
e quindi
![]()
![]() t
t![]() =
= ![]() -1
-1![]()
![]()
![]() f
f![]()
![]() = 2G0ej
= 2G0ej![]()
![]()
![]() f
f![]() ;
pertanto l'inviluppo complesso di
h
;
pertanto l'inviluppo complesso di
h![]() t
t![]() è un impulso di area
complessa
2G0ej
è un impulso di area
complessa
2G0ej![]() = 2G0
= 2G0![]() cos
cos![]() + jsin
+ jsin![]()
![]() .
All'uscita del canale
H
.
All'uscita del canale
H![]() f
f![]() troviamo quindi
troviamo quindi
| = | |||
| = | G0 |