Reti multistadio

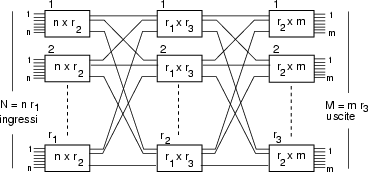
di cui in figura è riportato un esempio a 3 stadi, in cui gli N ingressi sono ripartiti su r₁ reti piú piccole con n ingressi, e le M uscite su r₃ reti con m uscite. Nel mezzo ci sono r₂ reti con r₁ ingressi ed r₃ uscite. Si può dimostrare che la rete complessiva è non bloccante se il numero di matrici dello stadio intermedio è almeno r₂ $\geq$ n + m - 1 (condizione di CLOS^4.44). Una connessione da sinistra a destra ha ora la possibilità di scegliere attraverso quale matrice intermedia passare.

0.600000

Nel caso di reti quadrate (N = M), ponendo n = m = $\sqrt{\frac{N}{2}}$, si ottiene un numero complessivo di incroci pari a 4$\left(\vphantom{ \sqrt{2}N^{\frac{3}{2}}-N}\right.$$\sqrt{2}$N^{${\frac{3}{2}}$} - N$\left.\vphantom{ \sqrt{2}N^{\frac{3}{2}}-N}\right)$, che risulta inferiore ad N² (e dunque vantaggioso rispetto ad un commutatore monostadio) a partire da N $\geq$ 24.

Ovviamente, la problematica relativa alle matrici di commutazione è molto articolata, coinvolgendo topologie piú complesse, filosofie di instradamento, e tecniche per la stima delle probabilità di blocco. Tralasciamo ulteriori approfondimenti, per illustrare invece come realizzare dispositivi di commutazione per trasmissioni numeriche a divisione di tempo.