




Avanti: Autocorrelazione
Su: Correlazione e Covarianza
Indietro: Covarianza e Indipendenza Statistica
Indice
Indice analitico
Nel caso in cui il processo da cui si estraggono x1 ed x2
sia stazionario, si ottiene che
e cioè la correlazione dipende solo dall'intervallo
 = t2 - t1.
Infatti se un processo è stazionario, le proprietà statistiche non dipendono
da traslazioni temporali.
= t2 - t1.
Infatti se un processo è stazionario, le proprietà statistiche non dipendono
da traslazioni temporali.
Nel caso in cui il processo sia anche ergodico, allora le medie di insieme
hanno lo stesso valore delle corrispondenti medie temporali, e dunque la correlazione
(media di insieme) può essere calcolata in base alla sua media temporale equivalente,
a partire da una qualunque realizzazione del processo
Ovviamente è vero anche l'inverso, e cioè: il valor medio del prodotto tra due
campioni, estratti (a caso) a distanza  a partire da una specifica
realizzazione7.7, ha un valore che è calcolabile come media di insieme a partire dalla conoscenza
della densità di probabilità congiunta
pX1X2
a partire da una specifica
realizzazione7.7, ha un valore che è calcolabile come media di insieme a partire dalla conoscenza
della densità di probabilità congiunta
pX1X2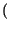 x1, x2;t1, t1 +
x1, x2;t1, t1 + 
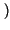 .
.





Avanti: Autocorrelazione
Su: Correlazione e Covarianza
Indietro: Covarianza e Indipendenza Statistica
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01