




Avanti: Autocorrelazione dell'uscita di un filtro
Su: Appendici
Indietro: Onda PAM
Indice
Indice analitico
Potenza di un segnale dati
Si è affermato che la potenza di un segnale
in cui
g t
t è una caratteristica di Nyquist a coseno rialzato
con roll-off
è una caratteristica di Nyquist a coseno rialzato
con roll-off 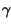 , e gli ai sono una sequenza di v.a. discrete,
statisticamente indipendenti, ed uniformemente distribuite su L livelli in una
dinamica
-
, e gli ai sono una sequenza di v.a. discrete,
statisticamente indipendenti, ed uniformemente distribuite su L livelli in una
dinamica
- 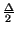
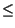 ai
ai 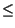
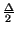 , ha valore
Nella precedente appendice, si è mostrato che per lo stesso segnale risulta
, ha valore
Nella precedente appendice, si è mostrato che per lo stesso segnale risulta
 s
s f
f =
= 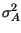
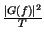 ,
e dunque
Svolgendo i relativi calcoli, si può mostrare che
,
e dunque
Svolgendo i relativi calcoli, si può mostrare che
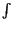
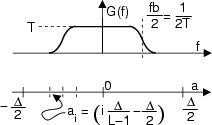
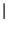 G
G f
f
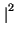 df = T
df = T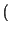 1 -
1 - 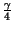
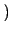 ,
e quindi
,
e quindi
 s =
s = 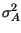
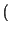 1 -
1 - 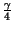
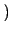 ;
resta pertanto da calcolare
;
resta pertanto da calcolare
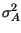 :
:
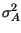 = (ai a media nulla)
= EX
= (ai a media nulla)
= EX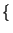 ai2
ai2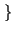 =
= 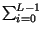 pai . ai2 =
(ai equiprobabili) =
pai . ai2 =
(ai equiprobabili) =
= 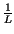
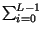
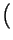 i
i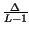 -
- 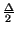
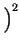 =
=
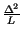
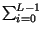
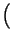
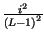 +
+ 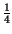 -
- 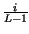
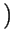 =
=
= 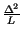
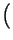
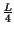 -
- 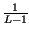
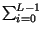 i +
i + 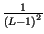
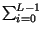
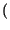 i
i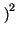
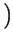 =
=
(facendo uso delle relazioni
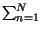 n =
n = 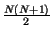 e
e
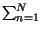 n2 =
n2 = 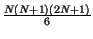 )
)
= 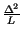
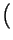
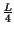 -
- 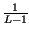
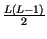 +
+ 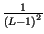
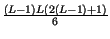
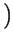 =
= 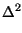
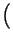
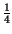 -
- 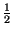 +
+ 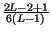
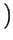 =
=
= 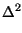
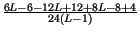 =
=
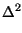
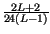 =
= 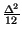
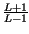 .
.





Avanti: Autocorrelazione dell'uscita di un filtro
Su: Appendici
Indietro: Onda PAM
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01

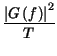 df
df
![]() = (ai a media nulla)
= EX
= (ai a media nulla)
= EX![]() ai2
ai2![]() =
= ![]() pai . ai2 =
(ai equiprobabili) =
pai . ai2 =
(ai equiprobabili) =