Convoluzione con l'impulso traslato

Consideriamo un sistema fisico che operi un semplice ritardo $\theta$ sui segnali in ingresso: in tal caso risulterà h$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\delta$$\left(\vphantom{ t-\theta }\right.$t - $\theta$ $\left.\vphantom{ t-\theta }\right)$ ovvero, la risposta all'impulso è un impulso ritardato.

Per calcolare l'uscita y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = x$\left(\vphantom{ t-\theta }\right.$t - $\theta$ $\left.\vphantom{ t-\theta }\right)$ possiamo ricorrere all'integrale di convoluzione, ottenendo

    y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$*$\delta$$\left(\vphantom{ t-\theta }\right.$t - $\theta$ $\left.\vphantom{ t-\theta }\right)$ =

     = $\int^{\infty }_{-\infty }$x$\left(\vphantom{ \tau }\right.$$\tau$ $\left.\vphantom{ \tau }\right)$ $\delta$$\left(\vphantom{ t-\theta -\tau }\right.$t - $\theta$ - $\tau$ $\left.\vphantom{ t-\theta -\tau }\right)$ d$\tau$ = x$\left(\vphantom{ t-\theta }\right.$t - $\theta$ $\left.\vphantom{ t-\theta }\right)$

 

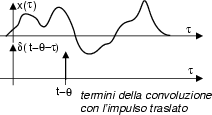
Questo risultato ci permette di enunciare un principio generale, che verrà utilizzato di frequente, e che recita:

La convoluzione tra un segnale x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ ed un impulso matematico $\delta$$\left(\vphantom{ t-\theta }\right.$t - $\theta$ $\left.\vphantom{ t-\theta }\right)$ centrato ad un istante $\theta$ provoca la traslazione di x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ all'istante in cui è centrato l'impulso.