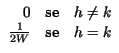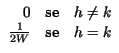next up previous contents index
Avanti: Uso pratico Su: Teorema del Campionamento Indietro: Aliasing   Indice   Indice analitico

Energia di un segnale campionato

Si puņ dimostrare che le funzioni sinc costituiscono una base di rappresentazione ortogonale, in quanto

$\displaystyle \int^{\infty }_{-\infty }$sinc$\displaystyle \left(\vphantom{ 2W\left( t-kT_{c}\right) }\right.$2W$\displaystyle \left(\vphantom{ t-kT_{c}}\right.$t - kTc$\displaystyle \left.\vphantom{ t-kT_{c}}\right)$ $\displaystyle \left.\vphantom{ 2W\left( t-kT_{c}\right) }\right)$sinc$\displaystyle \left(\vphantom{ 2W\left( t-hT_{c}\right) }\right.$2W$\displaystyle \left(\vphantom{ t-hT_{c}}\right.$t - hTc$\displaystyle \left.\vphantom{ t-hT_{c}}\right)$ $\displaystyle \left.\vphantom{ 2W\left( t-hT_{c}\right) }\right)$dt = $\displaystyle \left\{\vphantom{ \begin{array}{rcl} 0 & \hbox {se} & h\neq k\\ \frac{1}{2W} & \hbox {se} & h=k \end{array}}\right.$$\displaystyle \begin{array}{rcl} 0 & \hbox {se} & h\neq k\\ \frac{1}{2W} & \hbox {se} & h=k \end{array}$

Pertanto, il valore dell'energia di un segnale limitato in banda č calcolabile a partire dai suoi campioni, e vale:
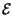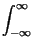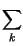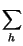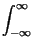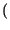$\displaystyle \mathcal {E}$x = $\displaystyle \int^{\infty }_{-\infty }$x$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$x*$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$dt = $\displaystyle \sum_{k}^{}$$\displaystyle \sum_{h}^{}$xkxh*$\displaystyle \int^{\infty }_{-\infty }$sinc$\displaystyle \left(\vphantom{ 2W\left( t-kT_{c}\right) }\right.$2W$\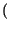displaystyle \left(\vphantom{ t-kT_{c}}\right.$t - kTc$\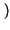displaystyle \left.\vphantom{ t-kT_{c}}\right)$ $\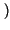displaystyle \left.\vphantom{ 2W\left( t-kT_{c}\right) }\right)$sinc$\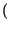displaystyle \left(\vphantom{ 2W\left( t-hT_{c}\right) }\right.$2W$\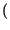displaystyle \left(\vphantom{ t-hT_{c}}\right.$t - hTc$\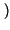displaystyle \left.\vphantom{ t-hT_{c}}\right)$ $\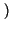displaystyle \left.\vphantom{ 2W\left( t-hT_{c}\right) }\right)$dt  
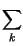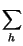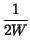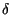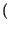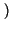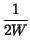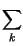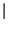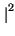  = $\displaystyle \sum_{k}^{}$$\displaystyle \sum_{h}^{}$xkxh*$\displaystyle {\frac{1}{2W}}$$\displaystyle \delta$$\displaystyle \left(\vphantom{ h,k}\right.$h, k$\displaystyle \left.\vphantom{ h,k}\right)$ = $\displaystyle {\frac{1}{2W}}$$\displaystyle \sum_{k}^{}$$\displaystyle \left\vert\vphantom{ x_{k}}\right.$xk$\displaystyle \left.\vphantom{ x_{k}}\right\vert^{2}_{}$  


alef@infocom.uniroma1.it
2001-06-01