Avanti: Condizioni di Nyquist
Su: Codifica di linea
Indietro: Codifica di linea
Indice
Indice analitico
Ci occupiamo ora del problema di trasmettere su di un canale analogico una informazione
che ``nasce'' discreta, a prescindere se derivi da un segnale campionato o
meno. Come vedremo, lo sviluppo analitico presenta alcuni aspetti in comune
con quello del teorema del campionamento.
Consideriamo allora una sorgente discreta, che produce simboli ak
ad una frequenza fs, con cui costruiamo un segnale
x t
t idoneo ad essere trasmesso su un canale analogico
idoneo ad essere trasmesso su un canale analogico
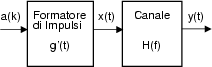
come illustrato nella figura che segue4.10. Un segnale siffatto Ŕ molto simile a quello giÓ illustrato dell'onda PAM,
e di nuovo occorre individuare una soluzione che tenga conto delle limitazioni
elencate al § 4.2.1.1.
0.400000
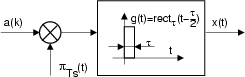
Costruzione dell' ONDA
DATI
![[*]](cross_ref_motif.gif) Ŕ piuttosto
semplice: basta utilizzare una risposta impulsiva
g
Ŕ piuttosto
semplice: basta utilizzare una risposta impulsiva
g t
t del
formatore di impulsi di tipo rettangolare:
g
del
formatore di impulsi di tipo rettangolare:
g t
t = rect
= rect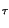
 t
t .
Pertanto, il segnale uscente dal formatore di impulsi risulta:
Come anticipato, questa soluzione ha lo svantaggio di occupare un banda infinita4.11 e quindi la sua trasmissione ``intatta'' Ŕ possibile solo per canali ideali4.12
.
.
Pertanto, il segnale uscente dal formatore di impulsi risulta:
Come anticipato, questa soluzione ha lo svantaggio di occupare un banda infinita4.11 e quindi la sua trasmissione ``intatta'' Ŕ possibile solo per canali ideali4.12
.
Prima di esporre una soluzione di compromesso a tutti
e 3 i problemi, consideriamo di inglobare in
g t
t sia l'effetto
del filtro di trasmissione che di quello del canale
H
sia l'effetto
del filtro di trasmissione che di quello del canale
H f
f ;
indichiamo pertanto il filtro di trasmissione come
g'
;
indichiamo pertanto il filtro di trasmissione come
g' t
t .
Con riferimento alla figura a lato, in (4.13) viene svolta la convoluzione tra
x
.
Con riferimento alla figura a lato, in (4.13) viene svolta la convoluzione tra
x t
t ed
h
ed
h t
t ,
che evidenzia come il segnale ricevuto
y
,
che evidenzia come il segnale ricevuto
y t
t abbia espressione
abbia espressione
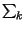 ak . g
ak . g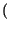 t - kTs
t - kTs , in cui
g
, in cui
g t
t = g'
= g' t
t *h
*h t
t .
Pertanto, i risultati che troveremo validi per
g
.
Pertanto, i risultati che troveremo validi per
g t
t individueranno
in realtÓ un formatore di impulsi con
G'
individueranno
in realtÓ un formatore di impulsi con
G' f
f =
= 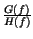 .
.





Avanti: Condizioni di Nyquist
Su: Codifica di linea
Indietro: Codifica di linea
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() t
t![]() idoneo ad essere trasmesso su un canale analogico
idoneo ad essere trasmesso su un canale analogico
![[*]](cross_ref_motif.gif) Ŕ piuttosto
semplice: basta utilizzare una risposta impulsiva
g
Ŕ piuttosto
semplice: basta utilizzare una risposta impulsiva
g