Processo ad Aleatorietà Parametrica

Questo è il nome dato a processi $\left\{\vphantom{ x\left( t,\theta \right) }\right.$x$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$ $\left.\vphantom{ x\left( t,\theta \right) }\right\}$ per quali il parametro $\theta$ compare in modo esplicito nella espressione analitica dei segnali membri. Come esempio, il segnale periodico x$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$ = $\sum_{n=-\infty }^{\infty }$A ^. tri_T(t - $\theta$ - nT), rappresentato in figura, ha come parametro un ritardo $\theta$, che è una variabile aleatoria che ne rende imprecisata la fase iniziale.

0.450000

Se $\theta$ è una v.a. uniformemente distribuita tra 0 e T (ovvero p_$\Theta$($\theta$) = ${\frac{1}{T}}$rect_T($\theta$ - ${\frac{T}{2}}$)), allora il processo è stazionario, ergodico, e la sua densità di probabilità risulta

p_X(x) = ${\frac{1}{A}}$rect_A(x - ${\frac{A}{2}}$)

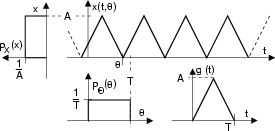
Il valor medio m_X = E$\left\{\vphantom{ x}\right.$x$\left.\vphantom{ x}\right\}$ è pari alla media temporale ${\frac{A}{2}}$, la varianza è quella della DDP^5.24 uniforme $\sigma_{X}^{2}$ = ${\frac{A^{2}}{12}}$ e la potenza vale $\mathcal {P}$_X = $\sigma_{X}^{2}$ + m_X² = ${\frac{A^{2}}{3}}$.

Se la p_$\Theta$($\theta$) fosse stata diversa, il processo avrebbe potuto perdere ergodicità. Se ad esempio p_$\Theta$($\theta$) = ${\frac{4}{T}}$rect_{${\frac{T}{4}}$}($\theta$), si sarebbe persa la stazionarietà: infatti prendendo ad esempio - ${\frac{T}{8}}$ < t < ${\frac{T}{8}}$, tutte le realizzazioni avrebbero valori minori del valor medio ${\frac{A}{2}}$.

Un secondo esempio di processo ad aleatorietà parametrica è il processo armonico, i cui membri hanno espressione x$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$ = Acos$\left(\vphantom{ 2\pi f_{0}t+\theta }\right.$2$\pi$f₀t + $\theta$ $\left.\vphantom{ 2\pi f_{0}t+\theta }\right)$, dove $\theta$ è una v.a. uniforme con DDP p_$\Theta$$\left(\vphantom{ \theta }\right.$$\theta$ $\left.\vphantom{ \theta }\right)$ = ${\frac{1}{2\pi }}$rect_2$\pi$$\left(\vphantom{ \theta }\right.$$\theta$ $\left.\vphantom{ \theta }\right)$. In tal caso il processo è stazionario ed ergodico, e si ottiene che una valore estratto a caso da un membro qualsiasi è una v.a. con DDP p_X$\left(\vphantom{ x}\right.$x$\left.\vphantom{ x}\right)$ = ${\frac{1}{\pi \sqrt{A^{2}+x^{2}}}}$.