




Avanti: Probabilità di Errore nelle Trasmissioni Numeriche
Su: Probabilità, Processi ed Errori
Indietro: Processo ad Aleatorietà Parametrica
Indice
Indice analitico
Trattiamo ora della questione, lasciata in sospeso, di come scegliere il numero
M di bit con cui rappresentare i campioni di un segnale, ovvero della
risoluzione con cui realizzare il dispositivo già indicato in 4.1.3
come quantizzatore. Tale processo consiste nel rappresentare i valori
x in ingresso mediante un insieme finito di L = 2M valori quantizzati
xq =
x +
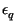
introducendo dunque un errore
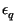 .
.
L'obiettivo
Figura:
Processo di quantizzazione per segnali
a distribuzione di ampiezza uniforme
|
|
è quello di scegliere L in modo da mantenere il rapporto segnale rumore
di quantizzazione SNRq migliore di un valore desiderato. Dato che
l'SNRq è pari al rapporto tra le potenze del segnale
 x
e del rumore
x
e del rumore

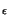 , procediamo nel determinare queste
ultime due, con l'aiuto del grafico mostrato in Fig. 5.1.
, procediamo nel determinare queste
ultime due, con l'aiuto del grafico mostrato in Fig. 5.1.
Adottiamo l'ipotesi semplificativa che i valori in ingresso al campionatore
abbiano origine da un processo ergodico a media nulla, e siano rappresentati
da una v.a. con densità di probabilità uniforme
pX(x) = 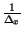 rect
rect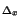 (x);
pertanto la potenza dei campioni, pari alla varianza della v.a., risulterà
(x);
pertanto la potenza dei campioni, pari alla varianza della v.a., risulterà
Lo stesso intervallo di valori di ingresso
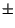
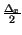 è suddiviso dal quantizzatore in L intervalli Ik di eguale
ampiezza
è suddiviso dal quantizzatore in L intervalli Ik di eguale
ampiezza
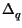 =
= 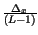 , centrati
sui valori
xk = k
, centrati
sui valori
xk = k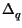 -
- 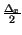 , con
k = 0, 1, 2,..., L - 1.
Tutti i valori di ingresso x, che cadono all'interno di Ik,
ovvero tali che
xk -
, con
k = 0, 1, 2,..., L - 1.
Tutti i valori di ingresso x, che cadono all'interno di Ik,
ovvero tali che
xk - 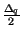
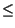 x < xk +
x < xk + 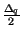 ,
sono codificati con l'intero k, rappresentato in binario da una parola
di
M = log2L bit.
,
sono codificati con l'intero k, rappresentato in binario da una parola
di
M = log2L bit.
Il componente che, a partire dai valori quantizzati, ricostruisce il segnale
xqo t
t da inviare al filtro di restituzione,
tipicamente associa ad ogni intero k il valore centrale
xq = xk
dell'intervallo di quantizzazione, commettendo cosí un errore
da inviare al filtro di restituzione,
tipicamente associa ad ogni intero k il valore centrale
xq = xk
dell'intervallo di quantizzazione, commettendo cosí un errore
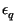 = xq - x,
di entità limitata entro l'intervallo
= xq - x,
di entità limitata entro l'intervallo
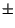
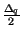 . Di nuovo,
si suppone che anche
. Di nuovo,
si suppone che anche
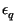 sia una v.a. uniformemente distribuita
tra
sia una v.a. uniformemente distribuita
tra
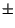
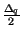 , ed indipendente5.25 da xk; pertanto, la potenza della componente di errore è anche qui
pari alla varianza, e cioè
, ed indipendente5.25 da xk; pertanto, la potenza della componente di errore è anche qui
pari alla varianza, e cioè
Siamo finalmente in grado di valutare l'SNR di quantizzazione:
in cui l'ultima approssimazione ha validità nel caso evidente in cui L 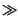 1.
Il risultato mostra che l'SNRq cresce in modo quadratico con l'aumentare
dei livelli, ovvero se L raddoppia SNRq quadruplica. Ricorrendo
alla notazione in decibel5.26 per l'SNR, otteniamo il risultato
1.
Il risultato mostra che l'SNRq cresce in modo quadratico con l'aumentare
dei livelli, ovvero se L raddoppia SNRq quadruplica. Ricorrendo
alla notazione in decibel5.26 per l'SNR, otteniamo il risultato
 SNRq
SNRq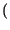 L
L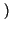
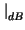 = 10log10L2 = 20log10L
e, ricordando che L = 2M, si ottiene
= 10log10L2 = 20log10L
e, ricordando che L = 2M, si ottiene
 SNRq
SNRq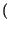 M
M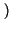
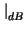
=
M . 10log
102
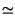
6
. M dB
dato che
log102 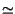 0.3. In modo simile, valutiamo il miglioramento
in dB ottenibile aumentando di uno il numero di bit per ogni campione, ovvero
raddoppiando il numero di livelli:
0.3. In modo simile, valutiamo il miglioramento
in dB ottenibile aumentando di uno il numero di bit per ogni campione, ovvero
raddoppiando il numero di livelli:
 SNRq
SNRq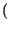 2L
2L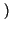
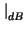 = 20log102L = 20log10L + 20log102
= 20log102L = 20log10L + 20log102 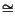
 SNRq
SNRq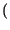 L
L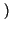
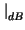 + 6 dB.
Pertanto ogni bit in più provoca un miglioramento di 6 dB per l'SNRq.
+ 6 dB.
Pertanto ogni bit in più provoca un miglioramento di 6 dB per l'SNRq.
Consideriamo ora cosa accade se il segnale in ingresso x ha una dinamica
minore di quanto previsto: in tal caso
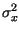 si riduce,
mentre
si riduce,
mentre
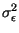 =
= 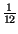
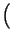
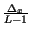
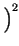 non cambia, e dunque SNRq peggiora come se avessimo ridotto i livelli.
non cambia, e dunque SNRq peggiora come se avessimo ridotto i livelli.





Avanti: Probabilità di Errore nelle Trasmissioni Numeriche
Su: Probabilità, Processi ed Errori
Indietro: Processo ad Aleatorietà Parametrica
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01


![]() rect
rect![]() (x);
pertanto la potenza dei campioni, pari alla varianza della v.a., risulterà
(x);
pertanto la potenza dei campioni, pari alla varianza della v.a., risulterà
![]() t
t![]() da inviare al filtro di restituzione,
tipicamente associa ad ogni intero k il valore centrale
xq = xk
dell'intervallo di quantizzazione, commettendo cosí un errore
da inviare al filtro di restituzione,
tipicamente associa ad ogni intero k il valore centrale
xq = xk
dell'intervallo di quantizzazione, commettendo cosí un errore
![]() = xq - x,
di entità limitata entro l'intervallo
= xq - x,
di entità limitata entro l'intervallo
![]()
![]() . Di nuovo,
si suppone che anche
. Di nuovo,
si suppone che anche
![]() sia una v.a. uniformemente distribuita
tra
sia una v.a. uniformemente distribuita
tra
![]()
![]() , ed indipendente5.25 da xk; pertanto, la potenza della componente di errore è anche qui
pari alla varianza, e cioè
, ed indipendente5.25 da xk; pertanto, la potenza della componente di errore è anche qui
pari alla varianza, e cioè
![]() si riduce,
mentre
si riduce,
mentre
![]() =
= ![]()
![]()
![]()
![]() non cambia, e dunque SNRq peggiora come se avessimo ridotto i livelli.
non cambia, e dunque SNRq peggiora come se avessimo ridotto i livelli.