




Avanti: Traffico, Code e Reti a Pacchetto
Su: Appendici
Indietro: Esercizio
Indice
Indice analitico
Prendiamo in considerazione una sorgente discreta, che emetta
simboli xk appartenenti ad un alfabeto di cardinalità L (ossia
con
k = 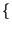 1, 2, ... , L
1, 2, ... , L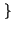 ), con probabilità
pk = Pr
), con probabilità
pk = Pr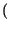 k
k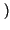 .
Definiamo l'informazione associata all'osservazione del simbolo xk
come5.41
.
Definiamo l'informazione associata all'osservazione del simbolo xk
come5.41
Ik =
I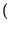 xk
xk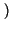
= log
2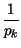
= - log
2pk
La scelta fatta, conduce ai seguenti risultati:
| Prob. |
Informazione |
Commento |
|---|
| pk |
-log2pk |
|
|---|
| 1 |
0 |
L'evento certo non fornisce informazione |
|---|
| 0 |
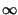 |
L'evento impossibile dà informazione infinita
|
|---|
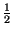 |
1 |
In caso di scelta binaria (es. testa o croce) occorre
una cifra binaria (bit = binary
digit ) per indicare il risultato |
|---|
<><>
L'informazione legata ad un evento è anche rappresentativa dell'incertezza a
suo riguardo, prima che questo si verifichi.
Passiamo ora a definire Entropia (indicata con H) di una sorgente
discreta S, il valore atteso dell'informazione apportata dalla conoscenza
dei simboli da essa generati:
che costituisce una interessante applicazione dell'operatore di valore
atteso da poco introdotto. H rappresenta l'informazione media
di un generico simbolo emesso dalla sorgente, ottenuta pesando l'informazione
di ogni possibile simbolo con la probabilità del simbolo stesso. Osserviamo
ora che:
- Se i simboli sono equiprobabili (
pk =
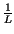 con
con 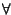 k),
la sorgente è massimamente informativa, e la sua entropia è la massima
possibile per un alfabeto ad L simboli, e cioè
HSMax =
k),
la sorgente è massimamente informativa, e la sua entropia è la massima
possibile per un alfabeto ad L simboli, e cioè
HSMax = 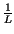
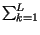 log2L = log2L.
log2L = log2L.
- Se i simboli non sono equiprobabili, allora
HS < log2L.
- Se la sorgente emette sempre e solo lo stesso simbolo, allora HS = 0.
Questa circostanza, assieme alla precedente, consente di scrivere che
0
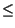 HS
HS 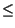 log2L.
log2L.
Un caso particolare è quello delle sorgenti binarie, che producono uno tra due
simboli
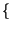 x0, x1
x0, x1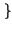 con probabilità rispettivamente
con probabilità rispettivamente
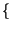 Pr
Pr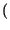 x0
x0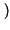 = p, Pr
= p, Pr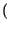 x1
x1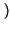 = q = 1 - p
= q = 1 - p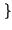 ,
che inserite nella formula dell'Entropia, forniscono l'espressione
,
che inserite nella formula dell'Entropia, forniscono l'espressione
Hb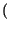 p
p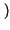
= -
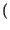 p
plog
2p +
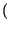
1 -
p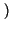
log
2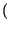
1 -
p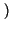
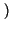
il cui andamento è mostrato nella figura seguente, in funzione di p.
Figura:
Entropia di sorgente binaria, e ridondanza associata
|
|
I due simboli
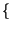 x0, x1
x0, x1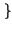 possono essere rappresentati
dalle 2 cifre binarie
possono essere rappresentati
dalle 2 cifre binarie
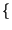 0, 1
0, 1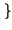 , che in questo caso chiamiamo
binit, per non confonderli con la misura dell'informazione (il bit),
ed allora se p
, che in questo caso chiamiamo
binit, per non confonderli con la misura dell'informazione (il bit),
ed allora se p 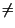 .5, usiamo 1 binit/simbolo per rappresentare un messaggio
con solo Hb < 1 bit/simbolo di informazione, dunque la nostra codifica
ha una ridondanza pari a
1 - Hb
.5, usiamo 1 binit/simbolo per rappresentare un messaggio
con solo Hb < 1 bit/simbolo di informazione, dunque la nostra codifica
ha una ridondanza pari a
1 - Hb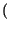 p
p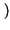 (graficata )5.42.
(graficata )5.42.
Lo stesso concetto, si applica ad una sorgente ad L livelli, con Entropia
HS = log2L, i cui simboli sono codificati con
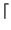 log2L
log2L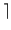 binit/simbolo5.43, con ridondanza
binit/simbolo5.43, con ridondanza
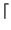 log2L
log2L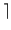 - HS. Ci chiediamo
allora: è possibile trasmettere tanti binit quanti ne servono, e non di più?
La risposta è sí, ricorrendo ad una CODIFICA DI SORGENTE, di cui appresso
forniamo un esempio.
- HS. Ci chiediamo
allora: è possibile trasmettere tanti binit quanti ne servono, e non di più?
La risposta è sí, ricorrendo ad una CODIFICA DI SORGENTE, di cui appresso
forniamo un esempio.
Consiste nell'usare CODEWORDS (parole di codice) di lunghezza
variabile, ed usare le più lunghe per i simboli meno probabili. Consideriamo
ad esempio una sorgente con alfabeto di cardinalità L = 4, ai cui simboli
compete la probabilità riportata nella tabella che segue. In questo caso l'Entropia
vale
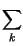 pk
pklog
2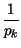
=
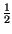
log
22 +
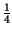
log
24 +
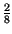
log
28 =
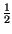
+
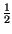
+
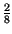
3 = 1.75
bit/
simbolo
mentre il numero medio di binit/simbolo usati è pari a
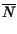 |
= |
E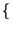 Lunghezza Lunghezza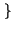 = = 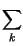 Lungh. Lungh.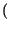 k k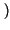 pk = pk = |
|
| |
= |
1 . 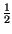 + 2 . + 2 . 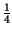 + 3 . + 3 . 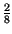 = 1.75 binit/simbolo = 1.75 binit/simbolo |
|
| Simbolo |
Prob. |
Codeword |
|---|
| x1 |
.5 |
1 |
|---|
| x2 |
.25 |
01 |
|---|
| x3 |
.125 |
001 |
|---|
| x4 |
.125 |
000 |
|---|
<><>
Osserviamo che:
- le codewords a lunghezza variabile non si confondono tra loro in quanto soddisfano
la regola del prefisso, ovvero nessuna codeword è uguale all'inizio di
una codeword più lunga: se cosí non fosse, non riusciremmo ad isolarle nel flusso
numerico.
- I due risultati (entropia e lunghezza media) coincidono, in virtú del fatto
che i valori di probabilità sono potenze non negative di 2.
Nel caso generale (valori di probabilità di emissione qualsiasi), si introduce
un ritardo di codifica, in modo da raggruppare più simboli di sorgente, ed effettuare
cosí una cosiddetta codifica a blocchi: per fissare le idee, consideriamo una
sorgente binaria, della quale si raggruppino coppie di bit simulando cosí una
sorgente a quattro valori. Con i risultati riportati in tabella che segue, si
può verificare che si ottiene una Entropia di sorgente
Hs = .8log
2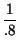
+ .2log
2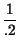
= 0.72
bit/simbolo, mentre adottando una codifica con 1 binit per ogni simbolo
generato, si ottiene ovviamente una lunghezza media di 1 binit/simbolo. Al contrario,
la lunghezza media ottenibile raggruppando coppie di simboli risulta pari a
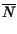
= 1
. .64 + 2
. .16 + 3
. .16 + 3
. .04 = 1.5792
binit/2 simboli, ossia pari a 0.7896 bit/simbolo.
| Simbolo |
Prob. |
Codeword |
|---|
| x1 |
.8 |
1 |
|---|
| x2 |
.2 |
0 |
|---|
|
x1x1 |
.64 |
1 |
|---|
|
x1x2 |
.16 |
01 |
|---|
|
x2x1 |
.16 |
001 |
|---|
|
x2x2 |
.04 |
000 |
|---|
<><>
In generale, prendendo blocchi via via più lunghi, è possibile ridurre la velocità
di codifica R (in binit/simbolo) rendendola sempre più simile all'Entropia,
ovvero
se la lunghezza del blocco tende ad infinito (Teorema di Shannon sulla
codifica di sorgente).
Sottosezioni





Avanti: Traffico, Code e Reti a Pacchetto
Su: Appendici
Indietro: Esercizio
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() 1, 2, ... , L
1, 2, ... , L![]() ), con probabilità
pk = Pr
), con probabilità
pk = Pr![]() k
k![]() .
Definiamo l'informazione associata all'osservazione del simbolo xk
come5.41
.
Definiamo l'informazione associata all'osservazione del simbolo xk
come5.41
![]() log2L
log2L![]() binit/simbolo5.43, con ridondanza
binit/simbolo5.43, con ridondanza
![]() log2L
log2L![]() - HS. Ci chiediamo
allora: è possibile trasmettere tanti binit quanti ne servono, e non di più?
La risposta è sí, ricorrendo ad una CODIFICA DI SORGENTE, di cui appresso
forniamo un esempio.
- HS. Ci chiediamo
allora: è possibile trasmettere tanti binit quanti ne servono, e non di più?
La risposta è sí, ricorrendo ad una CODIFICA DI SORGENTE, di cui appresso
forniamo un esempio.