




Avanti: Caratteristiche dei segnali
Su: Segnali e sistemi
Indietro: Segnali e sistemi
Indice
Indice analitico
Idealizziamo ora un sistema come una trasfomazione
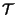
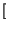 .
.![$ \left.\vphantom{ .}\right]$](img41.gif) ,
tale che ad ogni segnale di ingresso
x
,
tale che ad ogni segnale di ingresso
x t
t corrisponda una
uscita
y
corrisponda una
uscita
y t
t :
:
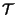
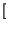 x
x t
t
![$ \left.\vphantom{ x\left( t\right) }\right]$](img43.gif) = y
= y t
t .
In base a tale formalismo, riportiamo alcune caratteristiche dei sistemi, che
ne descrivono il comportamento in termini più generali.
.
In base a tale formalismo, riportiamo alcune caratteristiche dei sistemi, che
ne descrivono il comportamento in termini più generali.
- Linearità
- Un sistema è lineare quando l'uscita associata ad una combinazione
lineare di ingressi, è la combinazione lineare delle uscite previste per ogni
singolo ingresso:
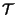
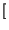
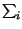 aixi
aixi t
t
![$ \left.\vphantom{ \sum _{i}a_{i}x_{i}\left( t\right) }\right]$](img46.gif) =
= 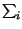 a
a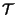
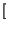 xi
xi t
t
![$ \left.\vphantom{ x_{i}\left( t\right) }\right]$](img48.gif) .
Al contrario, un legame ingresso-uscita senza memoria1.13
del tipo
y
.
Al contrario, un legame ingresso-uscita senza memoria1.13
del tipo
y t
t = g
= g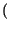 x
x t
t
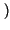 , in cui
g
, in cui
g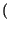 .
.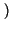 è una generica funzione non lineare1.14
.... non è lineare !
è una generica funzione non lineare1.14
.... non è lineare !
- Permanenza
- Un sistema è permanente (o stazionario) se l'uscita associata
ad un ingresso traslato nel tempo, è la traslazione temporale dell'uscita che
si avrebbe per lo stesso ingresso non traslato, ovvero: se
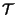
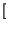 x
x t
t
![$ \left.\vphantom{ x\left( t\right) }\right]$](img43.gif) = y
= y t
t ,
allora
,
allora
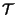
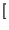 x
x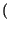 t -
t - 
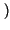
![$ \left.\vphantom{ x\left( t-\tau \right) }\right]$](img56.gif) = y
= y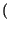 t -
t - 
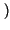 .
Nel caso contrario, il sistema è detto tempo-variante.
.
Nel caso contrario, il sistema è detto tempo-variante.
- Realizzabilità fisica
- E' detta anche causalità, perché consiste nel
non poter osservare una uscita, prima di aver applicato un qualunque ingresso.
Una definizione alternativa asserisce che i valori di uscita
y
 t
t ad un istante t = t0, non possono dipendere da valori di ingresso
x
ad un istante t = t0, non possono dipendere da valori di ingresso
x t
t per t > t0.
per t > t0.
- Stabilità
- è definita come la proprietà di fornire uscite limitate (in ampiezza)
per ingressi limitati.





Avanti: Caratteristiche dei segnali
Su: Segnali e sistemi
Indietro: Segnali e sistemi
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]()
![]() .
.![]() ,
tale che ad ogni segnale di ingresso
x
,
tale che ad ogni segnale di ingresso
x![]() t
t![]() corrisponda una
uscita
y
corrisponda una
uscita
y![]() t
t![]() :
:
![]()
![]() x
x![]() t
t![]()
![]() = y
= y![]() t
t![]() .
In base a tale formalismo, riportiamo alcune caratteristiche dei sistemi, che
ne descrivono il comportamento in termini più generali.
.
In base a tale formalismo, riportiamo alcune caratteristiche dei sistemi, che
ne descrivono il comportamento in termini più generali.