Caratteristiche dei segnali

Da un punto di vista analitico, un segnale è una funzione del tempo, del tipo descritto in 1.3, e per il quale si possono operare le classificazioni:

Segnale di potenza

Un segnale analogico può avere una estensione temporale limitata, oppure si può immaginare che si estenda da meno infinito a infinito. Nel secondo caso il segnale si dice di potenza se ne esiste (ed è diversa da zero) la media quadratica

0 < $\displaystyle \mathcal {P}$ _s = $\displaystyle \lim_{\Delta t\rightarrow \infty }^{}$ $\displaystyle {\frac{1}{\Delta t}}$ $\displaystyle \int^{\frac{\Delta t}{2}}_{-\frac{\Delta t}{2}}$ $\displaystyle \left\vert\vphantom{ s}\right.$ s $\displaystyle \left.\vphantom{ s}\right\vert^{2}_{}$ $\displaystyle \left(\vphantom{ t}\right.$ t $\displaystyle \left.\vphantom{ t}\right)$ dt < $\displaystyle \infty$

Segnale di energia

0 < $\displaystyle \mathcal {E}$ _s = $\displaystyle \int^{\infty }_{-\infty }$ $\displaystyle \left\vert\vphantom{ s}\right.$ s $\displaystyle \left.\vphantom{ s}\right\vert^{2}_{}$ $\displaystyle \left(\vphantom{ t}\right.$ t $\displaystyle \left.\vphantom{ t}\right)$ dt < $\displaystyle \infty$

Perché un segnale sia definito di energia occorre che $\int^{\infty }_{-\infty }$ $\left\vert\vphantom{ s\left( t\right) }\right.$ s $\left(\vphantom{ t}\right.$ t $\left.\vphantom{ t}\right)$ $\left.\vphantom{ s\left( t\right) }\right\vert^{2}_{}$ dt < $\infty$ , ovvero che s $\left(\vphantom{ t}\right.$ t $\left.\vphantom{ t}\right)$ tenda a zero (per t che tende ad $\infty$ ) più velocemente (od in modo uguale) ad ${\frac{1}{\sqrt{t}}}$ (e quindi $\left\vert\vphantom{ s\left( t\right) }\right.$ s $\left(\vphantom{ t}\right.$ t $\left.\vphantom{ t}\right)$ $\left.\vphantom{ s\left( t\right) }\right\vert^{2}_{}$ tenda a zero come ${\frac{1}{t}}$ ).

Esempi di segnali di energia

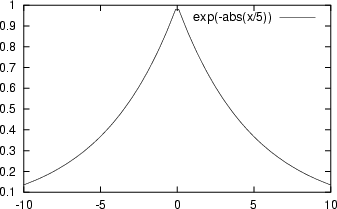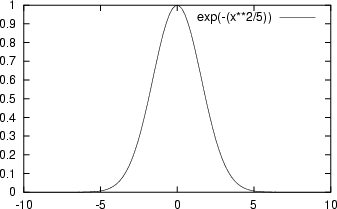$\includegraphics {cap1/f1.7.ps}$	$\includegraphics {cap1/f1.8.ps}$
Impulso Esponenziale Bilatero	Impulso Gaussiano

<><>

Segnale periodico

s $\displaystyle \left(\vphantom{ t}\right.$ t $\displaystyle \left.\vphantom{ t}\right)$ = s $\displaystyle \left(\vphantom{ t+T}\right.$ t + T $\displaystyle \left.\vphantom{ t+T}\right)$

Segnale di durata limitata

In particolare, se un segnale ha durata limitata - ovvero è nullo per t al di fuori di un intervallo $\left[\vphantom{ t_{1},t_{2}}\right.$ t₁, t₂ $\left.\vphantom{ t_{1},t_{2}}\right]$ - allora è anche di energia. Ad esempio:

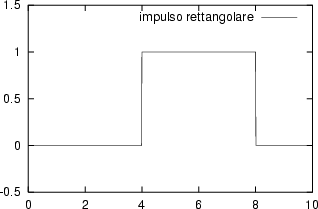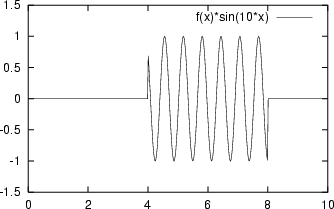$\includegraphics {cap1/f1.9.ps}$	$\includegraphics {cap1/f1.10.ps}$
Impulso rettangolare tra 4 ed 8	Sinusoide troncata

<><>

Segnale impulsivo

Se un segnale tende a zero come (o più velocemente di) ${\frac{1}{t}}$ , allora $\left\vert\vphantom{ s\left( t\right) }\right.$ s $\left(\vphantom{ t}\right.$ t $\left.\vphantom{ t}\right)$ $\left.\vphantom{ s\left( t\right) }\right\vert^{2}_{}$ tende a zero come (o più di) ${\frac{1}{t^{2}}}$ , e dunque è di energia. Questo caso particolare è chiamato segnale impulsivo.

Riassumendo

Qualora il segnale (come spesso nel nostro caso) sia associato a delle grandezze elettriche, allora i concetti di Potenza ed Energia hanno il correlato fisico illustrato di seguito.