




Avanti: Esempi
Su: Rappresentazione dei segnali modulati
Indietro: Filtro di Hilbert
Indice
Indice analitico
Il segnale analitico associato al segnale
x t
t corrisponde
al suo contenuto a frequenze positive
x+
corrisponde
al suo contenuto a frequenze positive
x+ t
t , che abbiamo
già introdotto; si può mostrare che
x+
, che abbiamo
già introdotto; si può mostrare che
x+ t
t è esprimibile
in termini di
è esprimibile
in termini di
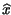
 t
t , secondo l'espressione8.15:
, secondo l'espressione8.15:
Molto utile è anche la relazione che lega il segnale analitico all'inviluppo
complesso:
che si ottiene tenendo conto dalla (8.1), come illustrato
alla nota8.16. Effettivamente, l'ultima relazione rappresenta il contenuto a frequenze positive
di
x t
t , a patto che
, a patto che
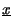
 t
t sia di banda base con frequenza massima W < f0; in tal caso infatti
si ottiene che, traformando la (8.2), risulta
che giace tutta nel semipiano f > 0.
sia di banda base con frequenza massima W < f0; in tal caso infatti
si ottiene che, traformando la (8.2), risulta
che giace tutta nel semipiano f > 0.
Per ottenere
x+ t
t (e da questo
(e da questo
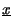
 t
t = 2x+
= 2x+ t
t e-j
e-j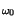 t),
anzichè utilizzare
t),
anzichè utilizzare
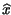
 t
t , si può pensare che
x+
, si può pensare che
x+ t
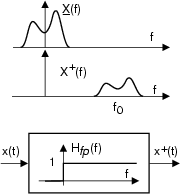
t sia il risultato del passaggio di
x
sia il risultato del passaggio di
x t
t attraverso un filtro
Hfp
attraverso un filtro
Hfp f
f 8.17 con funzione di trasferimento a gradino unitario:
8.17 con funzione di trasferimento a gradino unitario:
Invertendo la (8.2), otteniamo
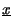
 t
t = 2x+
= 2x+ t
t e-j
e-j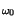 t,
che ci permette finalmente di valutare l'espressione di
t,
che ci permette finalmente di valutare l'espressione di
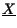
 f
f :
Ricordando ora che
:
Ricordando ora che
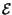 x
x f
f =
= 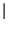 X
X f
f
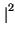 ,
otteniamo
,
otteniamo
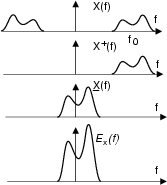
Un risultato del tutto simile può essere ottenuto per segnali di potenza, ovvero
Pertanto, la densità di potenza di
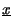
 t
t si ottiene da quella a frequenze positive di
x
si ottiene da quella a frequenze positive di
x t
t , traslata
nell'origine e moltiplicata per 4.
, traslata
nell'origine e moltiplicata per 4.





Avanti: Esempi
Su: Rappresentazione dei segnali modulati
Indietro: Filtro di Hilbert
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() t
t![]() corrisponde
al suo contenuto a frequenze positive
x+
corrisponde
al suo contenuto a frequenze positive
x+![]() t
t![]() , che abbiamo
già introdotto; si può mostrare che
x+
, che abbiamo
già introdotto; si può mostrare che
x+![]() t
t![]() è esprimibile
in termini di
è esprimibile
in termini di
![]()
![]() t
t![]() , secondo l'espressione8.15:
, secondo l'espressione8.15:
![]() t
t![]() (e da questo
(e da questo
![]()
![]() t
t![]() = 2x+
= 2x+![]() t
t![]() e-j
e-j![]() t),
anzichè utilizzare
t),
anzichè utilizzare
![]()
![]() t
t![]() , si può pensare che
x+
, si può pensare che
x+![]() t
t![]() sia il risultato del passaggio di
x
sia il risultato del passaggio di
x![]() t
t![]() attraverso un filtro
Hfp
attraverso un filtro
Hfp![]() f
f![]() 8.17 con funzione di trasferimento a gradino unitario:
8.17 con funzione di trasferimento a gradino unitario:
![]()
![]() t
t![]() si ottiene da quella a frequenze positive di
x
si ottiene da quella a frequenze positive di
x![]() t
t![]() , traslata
nell'origine e moltiplicata per 4.
, traslata
nell'origine e moltiplicata per 4.