Avanti: Serie di Fourier
Su: Prerequisiti trigonometrici
Indietro: Formule di Eulero
Indice
Indice analitico
Come è noto da altri corsi, un segnale del tipo
x t
t = Acos
= Acos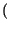 2
2 f0t +
f0t + 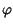
 è completamente rappresentato dal numero complesso
è completamente rappresentato dal numero complesso
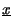 = Aej
= Aej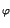 detto fasore, la cui conoscenza permette di riottenere il segnale originario
mediante la relazione
x
detto fasore, la cui conoscenza permette di riottenere il segnale originario
mediante la relazione
x t
t =
= 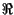
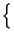
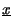 . ej2
. ej2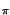 f0t
f0t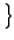 ,
che una volta sviluppata risulta infatti pari a
,
che una volta sviluppata risulta infatti pari a
x t t |
= |
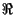 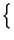 A . ej A . ej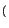 2 2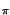 f0t + f0t + 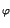 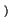 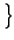 = A . = A . 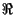 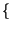 cos cos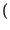 2 2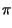 f0t + f0t + 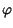 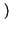 + jsin + jsin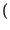 2 2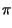 f0t + f0t + 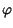 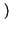 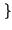 |
|
| |
= |
Acos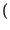 2 2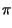 f0t + f0t + 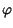  |
|
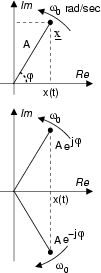
Osserviamo che il risultato ottenuto può interpretarsi graficamente come l'aver
impresso al fasore una rotazione di velocità angolare
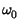 = 2
= 2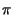 f0
radianti/secondo in senso antiorario, ed aver proiettato il risultato sull'asse
reale2.2. In alternativa, possiamo esprimere il segnale di partenza anche come
Tale operazione coinvolge anche le frequenze negative, e corrisponde
a tener conto anche di un secondo vettore rotante, che si muove ora in senso
orario, che ha una parte immaginaria di segno sempre opposto al primo, e che
è moltiplicato per il coniugato del fasore. Vedremo tra breve che l'ultima espressione
fornita è esattamente quella della serie di Fourier per il caso in questione.
f0
radianti/secondo in senso antiorario, ed aver proiettato il risultato sull'asse
reale2.2. In alternativa, possiamo esprimere il segnale di partenza anche come
Tale operazione coinvolge anche le frequenze negative, e corrisponde
a tener conto anche di un secondo vettore rotante, che si muove ora in senso
orario, che ha una parte immaginaria di segno sempre opposto al primo, e che
è moltiplicato per il coniugato del fasore. Vedremo tra breve che l'ultima espressione
fornita è esattamente quella della serie di Fourier per il caso in questione.





Avanti: Serie di Fourier
Su: Prerequisiti trigonometrici
Indietro: Formule di Eulero
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() t
t![]() = Acos
= Acos![]() 2
2![]() f0t +
f0t + ![]()
![]() è completamente rappresentato dal numero complesso
è completamente rappresentato dal numero complesso
![]() = Aej
= Aej![]() detto fasore, la cui conoscenza permette di riottenere il segnale originario
mediante la relazione
x
detto fasore, la cui conoscenza permette di riottenere il segnale originario
mediante la relazione
x![]() t
t![]() =
= ![]()
![]()
![]() . ej2
. ej2![]() f0t
f0t![]() ,
che una volta sviluppata risulta infatti pari a
,
che una volta sviluppata risulta infatti pari a