Avanti: Generazione di segnali BLU
Su: Modulazione di Ampiezza - AM
Indietro: Efficienza di PI-PPS
Indice
Indice analitico
Come abbiamo visto, la modulazione BLD determina una occupazione
di banda per x(t) doppia di quella di m(t). Per impegnare invece
una banda pari a quella di m(t), il segnale modulato deve dipendere da
entrambe le componenti analogiche xc(t) ed xs(t), che devono
risultare:
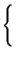
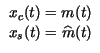 . Infatti in tal modo si ottiene:
. Infatti in tal modo si ottiene:
xBLU t t |
= |
m t t cos cos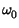 t - t - 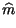  t t sin sin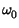 t = m t = m t t 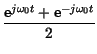 - - 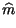  t t 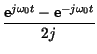 = = |
|
| |
= |
ej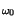 t t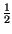 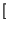 m m t t + j + j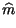  t t ![$\displaystyle \left.\vphantom{ m\left( t\right) +j\widehat{m}\left( t\right) }\right]$](img2685.gif) + e-j + e-j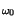 t t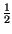 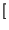 m m t t - j - j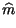  t t ![$\displaystyle \left.\vphantom{ m\left( t\right) -j\widehat{m}\left( t\right) }\right]$](img2687.gif) |
|
Ricordando ora che
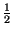
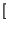 m
m t
t
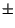 j
j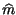
 t
t
![$ \left.\vphantom{ m\left( t\right) \pm j\widehat{m}\left( t\right) }\right]$](img2690.gif) = m
= m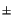
 t
t è proprio il contenuto a frequenze positive (negative), se x(t) è di
energia, effettuando la trasformata di Fourier di ambo i membri si ottiene
è proprio il contenuto a frequenze positive (negative), se x(t) è di
energia, effettuando la trasformata di Fourier di ambo i membri si ottiene
XBLU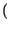 f f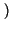 |
= |
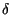 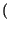 f - f0 f - f0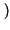 *M+ *M+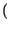 f f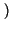 + + 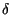 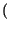 f + f0 f + f0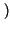 *M- *M-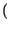 f f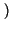 = = |
|
| |
= |
M+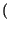 f - f0 f - f0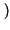 + M- + M-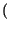 f + f0 f + f0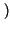 |
|
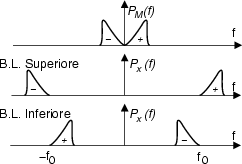
e quindi il segnale modulato AM-BLU è formato dai contenuti a frequenze
positive e negative di
m t
t , traslati ai lati della portante
f0.
, traslati ai lati della portante
f0.
Qualora si consideri invece
m t
t un processo, si può dimostrare
(passando dalla trasformata di
un processo, si può dimostrare
(passando dalla trasformata di
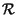 x
x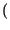

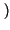 ) un
risultato del tutto analogo, ovvero
) un
risultato del tutto analogo, ovvero
Nel caso descritto abbiamo considerato soppressa la portante, ed il segnale
modulato (considerato nel dominio della frequenza) risulta ``esterno'' ad
f0: questa circostanza è indicata con il termine di banda laterale
superiore. Il caso opposto (banda laterale inferiore) si ottiene cambiando
segno a
xs t
t . Scriviamo dunque
con - e + rispettivamente per ottenere un segnale BLU con
banda superiore o inferiore. Con le costanti indicate, il segnale modulato BLU
ha una potenza
. Scriviamo dunque
con - e + rispettivamente per ottenere un segnale BLU con
banda superiore o inferiore. Con le costanti indicate, il segnale modulato BLU
ha una potenza
 x = 2 . (
x = 2 . (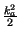 .
.  M .
M . 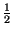 ) =
) = 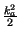
 M
(vedi 9.4.1), eguale a quella di un segnale AM-BLD in cui
xc(t) = kam
M
(vedi 9.4.1), eguale a quella di un segnale AM-BLD in cui
xc(t) = kam t
t e
xs(t) = 0.
e
xs(t) = 0.
I vantaggi di un tale metodo di modulazione sono subito evidenti: consente infatti
di risparmiare banda, permettendo la trasmissione di piú messaggi in divisione
di frequenza (FDM).
Sottosezioni





Avanti: Generazione di segnali BLU
Su: Modulazione di Ampiezza - AM
Indietro: Efficienza di PI-PPS
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
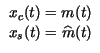 . Infatti in tal modo si ottiene:
. Infatti in tal modo si ottiene:
![]()
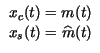 . Infatti in tal modo si ottiene:
. Infatti in tal modo si ottiene:
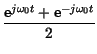 -
- 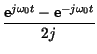 =
=![]() t
t![]() un processo, si può dimostrare
(passando dalla trasformata di
un processo, si può dimostrare
(passando dalla trasformata di
![]() x
x![]()
![]()
![]() ) un
risultato del tutto analogo, ovvero
) un
risultato del tutto analogo, ovvero