Demodulazione in fase e quadratura

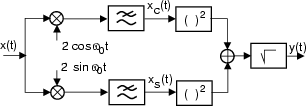
Se il demodulatore dispone anche del ramo in quadratura (quello con il seno) possiamo, in presenza di errore di fase, scegliere ad esempio quale dei due rami è meno attenuato, ed ovviare al problema. Lo stesso schema può essere utile in fase di ricerca della regione di frequenza in cui è presente un segnale^9.10, oppure qualora si desideri solo verificare la presenza o meno di un segnale ad una determinata frequenza, come nel caso del radar^9.11.

0.500000

 

 

Nel caso in cui il segnale ricevuto presenti una fase $\theta$ incognita

x$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = m$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$cos$$\left(\vphantom{ \omega _{0}t+\theta }\right.$$$$\omega_{0}^{}$$t + $$\theta$$ $$\left.\vphantom{ \omega _{0}t+\theta }\right)$$)

l'inviluppo complesso risulta

$$\underline{x}$$$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = m$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$e^j$\theta$ = m$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$cos$$\theta$$ + jm$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$sin$$\theta$$

e quindi x_c$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = m$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$cos$\theta$ e x_s$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = m$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$sin$\theta$.

Come noto, il demodulatore in fase e quadratura estrae proprio x_c$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ ed x_s$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, e dunque il segnale y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ risulta pari a:

y$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = $$\sqrt{x^{2}_{c}\left( t\right) +x^{2}_{s}\left( t\right) }$$ = $$\left\vert\vphantom{ m(t)}\right.$$m(t)$$\left.\vphantom{ m(t)}\right\vert$$$$\sqrt{\cos ^{2}\theta +\sin ^{2}\theta }$$ = $$\left\vert\vphantom{ m\left( t\right) }\right.$$m$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ $$\left.\vphantom{ m\left( t\right) }\right\vert$$

Pertanto, nonostante l'ignoranza della fase $\theta$, siamo ancora in grado di individuare la presenza di un segnale modulante. L'operazione di modulo impedisce l'uso dello schema per demodulare generici BLD-PS (mentre il caso PI sarebbe perfettamente demodulabile, ma in tal caso è piú che sufficiente un demodulatore di inviluppo (9.2.2)).