




Avanti: Demodulatore di inviluppo
Su: Demodulazione coerente (omodina)
Indietro: Demodulazione in fase e quadratura
Indice
Indice analitico
Trattiamo qui del problema di generare una portante di demodulazione
coerente (in fase) con quella della portante del segnale ricevuto. Una
soluzione molto usata si basa su di un circuito controreazionato che prende
il nome di anello ad aggancio di fase, e basa il suo funzionamento su
di un dispositivo chiamato oscillatore controllato in tensione (VCO,
VOLTAGE CONTROLLED OSCILLATOR).
Il VCO genera una sinusoide
y t
t = sin
= sin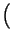
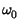 t + 2
t + 2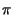 kf
kf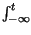 x
x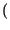

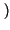 d
d
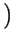 ,
la cui fase varia nel tempo con l'integrale del segnale di ingresso9.12.
,
la cui fase varia nel tempo con l'integrale del segnale di ingresso9.12.
Supponiamo ora di disporre di un segnale AM in cui sia presente un residuo di
portante, come ad esempio nel caso di portante parzialmente soppressa:
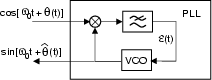
in tal caso la portante di demodulazione pu˛ essere ottenuta mediante il circuito
in figura, che prende il nome di PLL. Indicando con
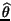
 t
t la fase giÓ integrata dal VCO fino all'istante t, all'uscita del moltiplicatore
Ŕ presente un segnale9.13:
Il termine centrato a frequenza doppia (
2
la fase giÓ integrata dal VCO fino all'istante t, all'uscita del moltiplicatore
Ŕ presente un segnale9.13:
Il termine centrato a frequenza doppia (
2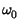 ) viene eliminato
dal filtro passa basso, e dunque rimane
in cui
) viene eliminato
dal filtro passa basso, e dunque rimane
in cui
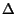
 rappresenta l'errore di fase, e
rappresenta l'errore di fase, e
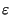 (t)
Ŕ la grandezza in ingresso al VCO. Qualora risulti
(t)
Ŕ la grandezza in ingresso al VCO. Qualora risulti
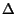
 = 0,
si ha che anche
= 0,
si ha che anche
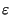 (t) = 0, ed il VCO non altera la fase (esatta)
della portante generata. Se
(t) = 0, ed il VCO non altera la fase (esatta)
della portante generata. Se
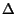
 > 0 (o
> 0 (o
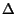
 < 0),
allora
< 0),
allora
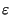
 t
t > 0 (o
> 0 (o
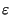
 t
t < 0)9.14, e dunque il VCO Ŕ portato ad aumentare (diminuire) la fase della propria portante
riducendo di conseguenza l'errore di fase9.15.
< 0)9.14, e dunque il VCO Ŕ portato ad aumentare (diminuire) la fase della propria portante
riducendo di conseguenza l'errore di fase9.15.
Nel caso in cui, invece, la fase entrante

 t
t vari
nel tempo, allora il PLL insegue tali variazioni tanto pi˙ da vicino quanto
pi˙ Ŕ elevato kf (il coefficiente di proporzionalitÓ tra
vari
nel tempo, allora il PLL insegue tali variazioni tanto pi˙ da vicino quanto
pi˙ Ŕ elevato kf (il coefficiente di proporzionalitÓ tra
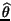
 t
t e l'integrale di
e l'integrale di
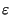
 t
t )9.16.
)9.16.





Avanti: Demodulatore di inviluppo
Su: Demodulazione coerente (omodina)
Indietro: Demodulazione in fase e quadratura
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() t
t![]() = sin
= sin![]()
![]() t + 2
t + 2![]() kf
kf![]() x
x![]()
![]()
![]() d
d![]()
![]() ,
la cui fase varia nel tempo con l'integrale del segnale di ingresso9.12.
,
la cui fase varia nel tempo con l'integrale del segnale di ingresso9.12.
![]()
![]() t
t![]() vari
nel tempo, allora il PLL insegue tali variazioni tanto pi˙ da vicino quanto
pi˙ Ŕ elevato kf (il coefficiente di proporzionalitÓ tra
vari
nel tempo, allora il PLL insegue tali variazioni tanto pi˙ da vicino quanto
pi˙ Ŕ elevato kf (il coefficiente di proporzionalitÓ tra
![]()
![]() t
t![]() e l'integrale di
e l'integrale di
![]()
![]() t
t![]() )9.16.
)9.16.