Prestazioni di QAM

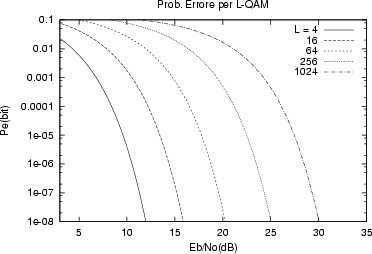
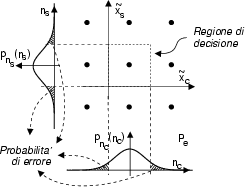
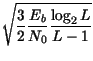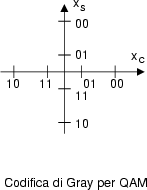Notiamo subito che la ``distanza'' tra due punti della costellazione QAM è maggiore (a parità di L) del caso PSK; pertanto, c'è da aspettarsi un miglioramento delle prestazioni (a parità di E_b/N₀) in quanto l'area che individua la probabilità di errore è ridotta. Il valore della probabilità di errore si determina dopo aver osservato che ciascuno dei due rami in fase e quadratura costituisce un segnale ASK multilivello con L' = $\sqrt{L}$.

Abbiamo già calcolato che, per tale segnale, il rapporto E_b/N₀ dopo demodulazione è esattamente pari a quello del segnale modulato; pertanto otteniamo

0.400000

$$\alpha \left(\vphantom{ simbolo}\right. \left.\vphantom{ simbolo}\right) \left(\vphantom{ simbolo}\right. \left.\vphantom{ simbolo}\right)$$ =

$$\left(\vphantom{ 1-\frac{1}{L'}}\right. {\frac{1}{L'}} \left.\vphantom{ 1-\frac{1}{L'}}\right) \left\{\vphantom{ \sqrt{3\frac{E_{b}}{N_{0}}\frac{\log _{2}L'}{\left( L'\right) ^{2}-1}}}\right. \sqrt{3\frac{E_{b}}{N_{0}}\frac{\log _{2}L'}{\left( L'\right) ^{2}-1}} \left.\vphantom{ \sqrt{3\frac{E_{b}}{N_{0}}\frac{\log _{2}L'}{\left( L'\right) ^{2}-1}}}\right\}$$ =

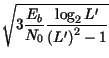Ricordando ora che L' = $\sqrt{L}$ = $\left(\vphantom{ L}\right.$L$\left.\vphantom{ L}\right)^{1/2}_{}$ e dunque log₂L' = ${\frac{1}{2}}$log₂L, si ottiene

P_$\alpha$ = $$\left(\vphantom{ 1-\frac{1}{\sqrt{L}}}\right.$$1 - $${\frac{1}{\sqrt{L}}}$$ $$\left.\vphantom{ 1-\frac{1}{\sqrt{L}}}\right)$$erfc$$\left\{\vphantom{ \sqrt{\frac{3}{2}\frac{E_{b}}{N_{0}}\frac{\log _{2}L}{L-1}}}\right.$$$$\sqrt{\frac{3}{2}\frac{E_{b}}{N_{0}}\frac{\log _{2}L}{L-1}}$$ $$\left.\vphantom{ \sqrt{\frac{3}{2}\frac{E_{b}}{N_{0}}\frac{\log _{2}L}{L-1}}}\right\}$$

La probabilità di errore (a carattere) complessiva, cioè la probabilità che il segnale ricevuto $\underline{\widetilde{x}}$ = $\underline{x}$ + $\underline{n}$ cada fuori della regione di decisione relativa all' $\underline{x}$ trasmesso, risulta P_e$\left(\vphantom{ carattere}\right.$carattere$\left.\vphantom{ carattere}\right)$ = P_$\alpha$ + P_$\alpha$ + $\left(\vphantom{ P_{\alpha }}\right.$P_$\alpha$$\left.\vphantom{ P_{\alpha }}\right)^{2}_{}$ $\simeq$ 2P_$\alpha$, in cui si assume trascurabile la probabilità di sbagliare entrambe x_c ed x_s.

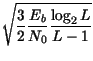
Questa stessa ipotesi, assieme all'utilizzo di un codice di Gray per codificare i gruppi di bit associati a livelli dei due rami, consente di esprimere la probabilità di errore per bit come

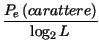P_e$$\left(\vphantom{ bit}\right.$$bit$$\left.\vphantom{ bit}\right)$$ = $${\frac{P_{e}\left( carattere\right) }{\log _{2}L}}$$ = $${\frac{2}{\log _{2}L}}$$$$\left(\vphantom{ 1-\frac{1}{\sqrt{L}}}\right.$$1 - $${\frac{1}{\sqrt{L}}}$$ $$\left.\vphantom{ 1-\frac{1}{\sqrt{L}}}\right)$$erfc$$\left\{\vphantom{ \sqrt{\frac{3}{2}\frac{E_{b}}{N_{0}}\frac{\log _{2}L}{L-1}}}\right.$$$$\sqrt{\frac{3}{2}\frac{E_{b}}{N_{0}}\frac{\log _{2}L}{L-1}}$$ $$\left.\vphantom{ \sqrt{\frac{3}{2}\frac{E_{b}}{N_{0}}\frac{\log _{2}L}{L-1}}}\right\}$$

Di seguito, sono raffigurate le curve con i valori di P_e$\left(\vphantom{ bit}\right.$bit$\left.\vphantom{ bit}\right)$ per diversi valori di L al variare di ${\frac{E_{b}}{N_{0}}}$ espresso in dB; il confronto con le curve relative al PSK permette di valutare l'entità del miglioramento di prestazioni. Come è evidente, la modulazione QAM offre prestazioni sensibilmente superiori rispetto alla PSK.