QAM

Questo acronimo, che sta per "Quadrature Amplitude Modulation", individua una tecnica di modulazione che utilizza (come il PSK) due portanti in quadratura. La differenza rispetto al PSK è che ora le componenti di banda base x_c ed x_s, che danno luogo a

x_QAM$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = x_c$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$cos$$\omega_{0}^{}$$t - x_s$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$sin$$\omega_{0}^{}$$t

non dipendono più da una stessa sequenza di fasi, ma sono originate da due flussi di dati distinti.

Modulatore QAM

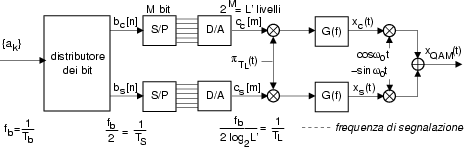
Nella pratica, questi due flussi di dati hanno origine da un medesimo messaggio numerico, i cui bit vengono distribuiti alternativamente sui due rami a frequenza metà. Questi vengono raggruppati per formare due segnali di banda base x_c ed x_s ad L' livelli, prodotti mediante un filtro formatore di impulsi G$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ che determina l'occupazione spettrale del segnale x_QAM ottenuto a partire da x_c ed x_s mediante modulazione in fase e quadratura. Se G$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ è a coseno rialzato con roll off $\gamma$, allora la banda a frequenze positive di x_QAM risulta pari a ${\frac{f_{b}}{2\log _{2}L'}}$$\left(\vphantom{ 1+\gamma }\right.$1 + $\gamma$ $\left.\vphantom{ 1+\gamma }\right)$ Hz.

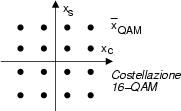
La sequenza di operazioni determina una costellazione quadrata, composta da L = $\left(\vphantom{ L'}\right.$L'$\left.\vphantom{ L'}\right)^{2}_{}$ punti, che rappresentano le coordinate, nel piano dell'inviluppo complesso, in cui quest'ultimo è forzato a transitare in corrispondenza degli istanti di Nyquist multipli di T_L.

In definitiva, il periodo di simbolo risulta

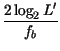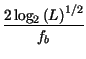T_L = $${\frac{2\log _{2}L'}{f_{b}}}$$ = $${\frac{2\log _{2}\left( L\right) ^{1/2}}{f_{b}}}$$ = $${\frac{1}{f_{b}}}$$log₂L

mentre la banda occupata è

B = f_L$$\left(\vphantom{ 1+\gamma }\right.$$1 + $$\gamma$$ $$\left.\vphantom{ 1+\gamma }\right)$$ = $${\frac{f_{b}}{\log _{2}L}}$$$$\left(\vphantom{ 1+\gamma }\right.$$1 + $$\gamma$$ $$\left.\vphantom{ 1+\gamma }\right)$$

e quindi uguale al PSK con uguale numero di livelli (di cui condivide quindi anche l'efficienza spettrale). Notiamo che, per come si è impostato lo schema di distribuzione dei bit tra i rami, L deve risultare un quadrato perfetto. Nulla impedisce di elaborare schemi più complessi in cui L' è diverso per i due rami, oppure in cui la costellazione non sia quadrata.