FSK Ortogonale

A pagina è stata introdotta la modulazione FSK, e nelle note si è iniziata la discussione relativa alle condizioni di ortogonalità tra le frequenze di confronto ed il segnale ricevuto; prendiamo qui in considerazione segnali del tipo generale cos$\left[\vphantom{ 2\pi \left( f_{0}+\Delta f_{k}\right) t+\phi _{k}}\right.$2$\pi$$\left(\vphantom{ f_{0}+\Delta f_{k}}\right.$f₀ + $\Delta$f_k$\left.\vphantom{ f_{0}+\Delta f_{k}}\right)$t + $\phi_{k}^{}$ $\left.\vphantom{ 2\pi \left( f_{0}+\Delta f_{k}\right) t+\phi _{k}}\right]$, in cui è incluso un errore di fase aleatorio tra simboli, in modo da esaminare le differenze tra il caso di modulazione coerente ed incoerente.

Iniziamo dunque con lo sviluppare l'espressione dell'integrale di intercorrelazione $\rho$ = $\int_{0}^{T_{L}}$cos$\left[\vphantom{ 2\pi \left( f_{0}+m\Delta \right) t}\right.$2$\pi$$\left(\vphantom{ f_{0}+m\Delta }\right.$f₀ + m$\Delta$ $\left.\vphantom{ f_{0}+m\Delta }\right)$t$\left.\vphantom{ 2\pi \left( f_{0}+m\Delta \right) t}\right]$cos$\left[\vphantom{ 2\pi \left( f_{0}+n\Delta \right) t+\phi }\right.$2$\pi$$\left(\vphantom{ f_{0}+n\Delta }\right.$f₀ + n$\Delta$ $\left.\vphantom{ f_{0}+n\Delta }\right)$t + $\phi$ $\left.\vphantom{ 2\pi \left( f_{0}+n\Delta \right) t+\phi }\right]$dt facendo uso della relazione cos$\alpha$cos$\beta$ = ${\frac{1}{2}}$$\left[\vphantom{ \cos \left( \alpha +\beta \right) \cos \left( \alpha -\beta \right) }\right.$cos$\left(\vphantom{ \alpha +\beta }\right.$$\alpha$ + $\beta$ $\left.\vphantom{ \alpha +\beta }\right)$cos$\left(\vphantom{ \alpha -\beta }\right.$$\alpha$ - $\beta$ $\left.\vphantom{ \alpha -\beta }\right)$ $\left.\vphantom{ \cos \left( \alpha +\beta \right) \cos \left( \alpha -\beta \right) }\right]$ e riferendoci per semplicità al caso di due frequenze contigue (ponendo m = 0 ed n = 1):

$$\rho {\textstyle\frac{1}{2}} \int_{0}^{T_{L}} \left\{\vphantom{ \cos \left[ 2\pi \left( 2f_{0}+\Delta \right) t+\phi \right] +\cos \left[ 2\pi \Delta t-\phi \right] }\right. \left[\vphantom{ 2\pi \left( 2f_{0}+\Delta \right) t+\phi }\right. \pi \left(\vphantom{ 2f_{0}+\Delta }\right. \Delta \left.\vphantom{ 2f_{0}+\Delta }\right) \phi \left.\vphantom{ 2\pi \left( 2f_{0}+\Delta \right) t+\phi }\right] \left[\vphantom{ 2\pi \Delta t-\phi }\right. \pi \Delta \phi \left.\vphantom{ 2\pi \Delta t-\phi }\right] \left.\vphantom{ \cos \left[ 2\pi \left( 2f_{0}+\Delta \right) t+\phi \right] +\cos \left[ 2\pi \Delta t-\phi \right] }\right\}$$ = (11.1)

$${\textstyle\frac{1}{2}} \int_{0}^{T_{L}} \left[\vphantom{ 2\pi \left( 2f_{0}+\Delta \right) t+\phi }\right. \pi \left(\vphantom{ 2f_{0}+\Delta }\right. \Delta \left.\vphantom{ 2f_{0}+\Delta }\right) \phi \left.\vphantom{ 2\pi \left( 2f_{0}+\Delta \right) t+\phi }\right] {\textstyle\frac{1}{2}} \int_{0}^{T_{L}} \left[\vphantom{ 2\pi \Delta t-\phi }\right. \pi \Delta \phi \left.\vphantom{ 2\pi \Delta t-\phi }\right]$$ = (11.2)

Per quanto riguarda il primo integrale, esso assume un valore nullo se 2f₀ + $\Delta$ = ${\frac{k}{T_{L}}}$, perché in tal caso in un intervallo T_L entrano un numero intero di periodi, ed il coseno ha valor medio nullo. Concentriamoci allora sul valore di $\Delta$ che annulla anche il secondo integrale, che riscriviamo facendo uso della relazione cos$\left(\vphantom{ \alpha -\beta }\right.$$\alpha$ - $\beta$ $\left.\vphantom{ \alpha -\beta }\right)$ = cos$\alpha$cos$\beta$ + sin$\alpha$sin$\beta$:

$$\int_{0}^{T_{L}} \left(\vphantom{ 2\pi \Delta t-\phi }\right. \pi \Delta \phi \left.\vphantom{ 2\pi \Delta t-\phi }\right) \int_{0}^{T_{L}} \left[\vphantom{ \cos \left( 2\pi \Delta t\right) \cos \phi +\sin \left( 2\pi \Delta t\right) \sin \phi }\right. \left(\vphantom{ 2\pi \Delta t}\right. \pi \Delta \left.\vphantom{ 2\pi \Delta t}\right) \phi \left(\vphantom{ 2\pi \Delta t}\right. \pi \Delta \left.\vphantom{ 2\pi \Delta t}\right) \phi \left.\vphantom{ \cos \left( 2\pi \Delta t\right) \cos \phi +\sin \left( 2\pi \Delta t\right) \sin \phi }\right]$$ = (11.3)

$$\left.\vphantom{ \frac{\sin \left( 2\pi \Delta t\right) }{2\pi \Delta }}\right. {\frac{\sin \left( 2\pi \Delta t\right) }{2\pi \Delta }} \left.\vphantom{ \frac{\sin \left( 2\pi \Delta t\right) }{2\pi \Delta }}\right\vert _{0}^{T_{L}} \phi \left.\vphantom{ \frac{\cos \left( 2\pi \Delta t\right) }{2\pi \Delta }}\right. {\frac{\cos \left( 2\pi \Delta t\right) }{2\pi \Delta }} \left.\vphantom{ \frac{\cos \left( 2\pi \Delta t\right) }{2\pi \Delta }}\right\vert _{0}^{T_{L}} \phi$$ = (11.4)

$$\left[\vphantom{ \frac{\sin \left( 2\pi \Delta T_{L}\right) }{2\p... ...os \left( 2\pi \Delta T_{L}\right) }{2\pi \Delta T_{L}}\cdot \sin \phi }\right. {\frac{\sin \left( 2\pi \Delta T_{L}\right) }{2\pi \Delta T_{L}}} \phi {\frac{1-\cos \left( 2\pi \Delta T_{L}\right) }{2\pi \Delta T_{L}}} \phi \left.\vphantom{ \frac{\sin \left( 2\pi \Delta T_{L}\right) }{2\p... ...os \left( 2\pi \Delta T_{L}\right) }{2\pi \Delta T_{L}}\cdot \sin \phi }\right]$$ = (11.5)

Osserviamo ora che, nel caso in cui $\phi$ = 0, il secondo termine si annulla per qualunque $\Delta$. Esaminiamo quindi ora solamente il primo termine, individuando così il risultato relativo al caso di

Modulazione coerente

Il termine ${\frac{\sin \left( 2\pi \Delta T_{L}\right) }{2\pi \Delta T_{L}}}$ si annulla per $\Delta$ = ${\frac{k}{2T_{L}}}$, e quindi la minima spaziatura tra portanti risulta $\Delta$ = ${\frac{1}{2T_{L}}}$ = ${\frac{f_{L}}{2}}$; pertanto, le frequenze utilizzate dovranno essere del tipo f₀ + k${\frac{f_{L}}{2}}$.

Per quanto riguarda il primo termine della 11.2, anche questo si annulla se sussiste la relazione 2f₀ + $\Delta$ = 2f₀ + ${\frac{f_{L}}{2}}$ = ${\frac{k}{T_{L}}}$ = kf_L, che fornisce la condizione f₀ = f_L${\frac{2k-1}{4}}$, ossia f₀ = ${\frac{1}{4}}$f_L, ${\frac{3}{4}}$f_L, ${\frac{5}{4}}$f_L, ${\frac{7}{4}}$f_L,.... Notiamo come la spaziatura ${\frac{f_{L}}{2}}$ tra i possibili valori per la portante, coincida con quella tra le frequenze di segnalazione. Pertanto la parte sinistra della figura 11.1 rappresenta,

Figura: d'onda ortogonali nei casi di modulazione coerente ed incoerente

        

disegnate in un intervallo pari a T_L, sia le portanti che possono essere usate, sia le prime frequenze che è possibile adottare per un modulazione FSK coerente basata sul valore minimo di f₀ pari a ${\frac{1}{4}}$f_L.

Nel caso in cui f₀ non assuma uno dei valori individuati, il primo termine di 11.2 non si annulla, ma se f₀ $\gg$ ${\frac{1}{T_{L}}}$, risulta trascurabile rispetto al secondo. Pertanto, nel caso di trasmissioni su canali di tipo passa-banda, la scelta di f₀ non è più determinante; d'altra parte, la spaziatura tra le frequenze di segnalazione pari a ${\frac{f_{L}}{2}}$ produce comunque il risultato che due frequenze di segnalazione contigue, accumulano in un intervallo T_L una differenza di fase di mezzo periodo.

Modulazione incoerente

In questo caso si ha $\phi$ $\neq$ 0. In generale la 11.5 presenta entrambi i termini; mentre il primo (come ora esaminato) si annulla per $\Delta$ = ${\frac{k}{2T_{L}}}$, il secondo invece è nullo solo se $\Delta$ = ${\frac{k}{T_{L}}}$. Questa circostanza determina il risultato che occorre ora adottare una spaziatura tra portati doppia della precedente, e pari cioè a $\Delta$ = f_L.

Tornando ad esaminare la 11.2, il suo primo termine si annulla ora se 2f₀ + $\Delta$ = 2f₀ + f_L = kf_L, che determina la condizione f₀ = f_L${\frac{k-1}{2}}$, ossia f₀ = 0, ${\frac{1}{2}}$f_L, f_L, ${\frac{3}{2}}$f_L,....Notiamo come la spaziatura ${\frac{f_{L}}{2}}$ tra i possibili valori per la portante sia identica al caso precedente, ma sia ora pari alla metà della spaziatura necessaria alle frequenze di segnalazione. La circostanza che sia adesso ammessa anche una portante a frequenza nulla consente di tracciare la parte destra della figura 11.1, che mostra le prime frequenze di segnalazione che è possibile adottare per una modulazione FSK incoerente basata sul valore minimo di f₀ = 0.

Verifica grafica

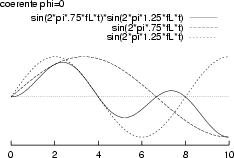
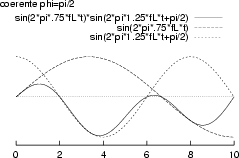
La figura che segue mostra il risultato del prodotto di due frequenze ortogonali distanti ${\frac{f_{L}}{2}}$ e calcolate in assenza di errore di fase (a sinistra) e con un errore di fase pari a $\phi$ = ${\frac{\pi }{2}}$. Si può notare come in questo secondo caso si perda l'ortogonalità tra i segnali, essendo il risultato prevalentemente negativo.

        

Discussione sull'ottimalità per L $\rightarrow$ $\infty$

Osserviamo innanzitutto che il ricevitore a correlazione commette errore nel caso in cui il rumore sovrapposto al segnale di ingresso sia casualmente ``simile'' ad una delle cosinusoidi utilizzate per la trasmissione. In tal caso, l'uscita dell'integratore relativo alla frequenza ``simile'' può superare quella relativa alla frequenza trasmessa.

All'aumentare di L (per f_b fisso) aumenta il periodo di simbolo T_L = ${\frac{\log _{2}L}{f_{b}}}$ e quindi diventa sempre più ``difficile'' per il rumore emulare ``bene'' una della frequenze di segnalazione, e quindi si riduce la probabilità di errore.

Chiaramente, all'aumentare di L aumenta proporzionalmente la complessità del ricevitore, che deve disporre di un numero di correlatori crescente. Pertanto, le prestazioni ideali per L che tende ad infinito rivestono solamente un interesse teorico.