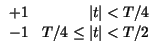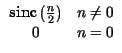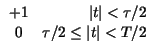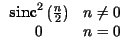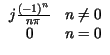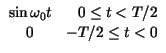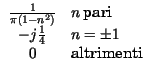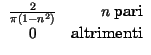Avanti: Trasformata di Fourier
Su: Appendice
Indietro: Algebra Vettoriale
Indice
Indice analitico
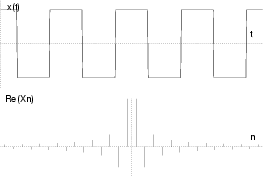
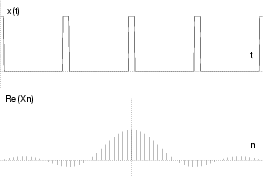
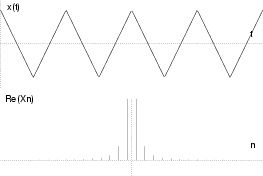
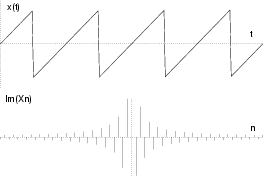
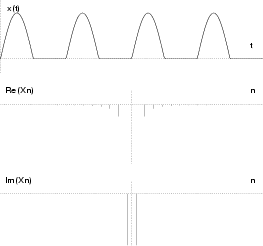
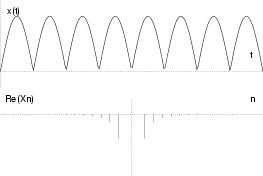
Nello schema che segue, sono mostrate le ampiezze delle componenti armoniche
Xn per alcuni segnali periodici di periodo T, di cui è fornita
l'epressione nel tempo per
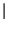 t
t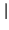 < T/2.
< T/2.
Xn =
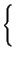
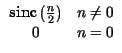
Xn =
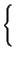
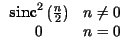
Xn =
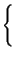
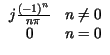
Xn =
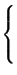
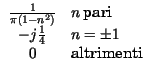
Xn =
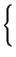
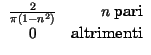
Sottosezioni





Avanti: Trasformata di Fourier
Su: Appendice
Indietro: Algebra Vettoriale
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() t
t![]() < T/2.
< T/2.