Costanti distribuite, grandezze derivate, e condizioni generali

 

0.300000

 Un conduttore elettrico uniforme e di lunghezza infinita, è descritto in base ad un modello a costanti distribuite, espresso in termini delle costanti primarie costituite dalla resistenza r, la conduttanza g, la capacità c e l'induttanza l per unità di lunghezza. La teoria delle linee uniformi definisce quindi due grandezze derivate dalle costanti primarie: l'impedenza caratteristica Z₀$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ e la costante di propagazione $\gamma$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$.

Impedenza caratteristica

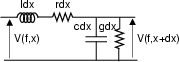
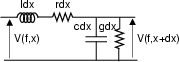
E' definita come

Z₀$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = R₀$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ + jX₀$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = $$\sqrt{\frac{r+j2\pi fl}{g+j2\pi fc}}$$

e rappresenta il rapporto tra V$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ ed I$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ in un generico punto del cavo, permettendo di scrivere I$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{V\left( f\right) }{Z_{0}\left( f\right) }}$.

Costante di propagazione

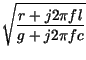
E' definita come

$$\gamma$$$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = $$\alpha$$$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ + j$$\beta$$$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = $$\sqrt{\left( r+j2\pi fl\right) \left( g+j2\pi fc\right) }$$

mentre la grandezza e^{- $\gamma$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$d} rappresenta il rapporto dei valori di tensione presenti tra due punti di un cavo di lunghezza infinita, distanti d, permettendo di scrivere: V$\left(\vphantom{ f,x+d}\right.$f, x + d$\left.\vphantom{ f,x+d}\right)$ = e^{- $\gamma$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$d}V$\left(\vphantom{ f,x}\right.$f, x$\left.\vphantom{ f,x}\right)$.

Condizioni di chiusura

Qualora il cavo di lunghezza d sia chiuso ai suoi estremi su di un generatore con impedenza Z_g$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ e su di un carico Z_c$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$, risultano definiti i coefficienti di riflessione del generatore e del carico:

$$\left(\vphantom{ f}\right. \left.\vphantom{ f}\right) {\frac{Z_{g}\left( f\right) -Z_{0}\left( f\right) }{Z_{g}\left( f\right) +Z_{0}\left( f\right) }} \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) {\frac{Z_{c}\left( f\right) -Z_{0}\left( f\right) }{Z_{c}\left( f\right) +Z_{0}\left( f\right) }}$$ (13.1)

Osserviamo subito che nel caso in cui Z_g$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Z_c$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Z₀$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$, risulta r_g$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = r_c$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = 0.

Quadripolo equivalente

L'impedenza vista dai morsetti di ingresso e di uscita di un cavo, interposto tra generatore e carico, vale rispettivamente

$$\left(\vphantom{ f}\right. \left.\vphantom{ f}\right) \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) {\frac{1+r_{c}\left( f\right) \cdot \hbox {e}^{-d\gamma \left( f\right) }}{1-r_{c}\left( f\right) \cdot \hbox {e}^{-d\gamma \left( f\right) }}} \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) {\frac{1+r_{g}\left( f\right) \cdot \hbox {e}^{-d\gamma \left( f\right) }}{1-r_{g}\left( f\right) \cdot \hbox {e}^{-d\gamma \left( f\right) }}}$$ (13.2)

Allo stesso tempo, la funzione di trasferimento intrinseca risulta

$$\left(\vphantom{ f}\right. \left.\vphantom{ f}\right) {\frac{\hbox {e}^{-d\gamma \left( f\right) }}{1-r_{g}\left( f\right) \cdot r_{c}\left( f\right) \cdot \hbox {e}^{-2d\gamma \left( f\right) }}}$$ (13.3)

Condizioni di adattamento

Nel caso in cui Z_g$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Z_c$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Z₀$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$, come sappiamo, il quadripolo si comporta in modo perfetto. In tal caso, risultando r_g$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = r_c$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = 0, si ottiene che Z_i$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Z_u$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Z₀$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ e H_q$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{V_{q}\left( f\right) }{V_{i}\left( f\right) }}$ = 2e^{-d$\gamma$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$}: il cavo si comporta allora come se avesse lunghezza infinita. In tal caso, inoltre, risulta che H_i$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{1}{2}}$ ed R_g$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = R_u$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$; pertanto il guadagno disponibile risulta

G_d$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = $$\left\vert\vphantom{ H_{i}\left( f\right) }\right.$$H_i$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ $$\left.\vphantom{ H_{i}\left( f\right) }\right\vert^{2}_{}$$$$\left\vert\vphantom{ H_{q}\left( f\right) }\right.$$H_q$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ $$\left.\vphantom{ H_{q}\left( f\right) }\right\vert^{2}_{}$$$${\frac{R_{g}\left( f\right) }{R_{u}\left( f\right) }}$$ = $${\textstyle\frac{1}{4}}$$$$\left\vert\vphantom{ 2\hbox {e}^{-d\left[ \alpha \left( f\right) +j\beta \left( f\right) \right] }}\right.$$2e^{-d$\left[\vphantom{ \alpha \left( f\right) +j\beta \left( f\right) }\right.$$\alpha$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ + j$\beta$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ \alpha \left( f\right) +j\beta \left( f\right) }\right]$}$$\left.\vphantom{ 2\hbox {e}^{-d\left[ \alpha \left( f\right) +j\beta \left( f\right) \right] }}\right\vert^{2}_{}$$ = e^{-2d$\alpha$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$}

Condizione di Heaviside

Nel caso in cui i valori delle costanti primarie sia tale da risultare r ^. c = l ^. g, note come condizioni di Heaviside, allora per la costante di propagazione si ottiene $\gamma$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\alpha$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ + j$\beta$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\sqrt{rg}$ + j2$\pi$f$\sqrt{lc}$: pertanto, $\alpha$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ è costante e $\beta$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ cresce linearmente con la frequenza, realizzando così le condizioni di un canale perfetto, in quanto H_q$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = 2e^{-d$\alpha$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$}e^{-jd$\beta$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$} = 2e^{-d$\sqrt{rg}$}e^{-jd2$\pi$f$\sqrt{lc}$}.

Allo stesso tempo, l'impedenza caratteristica Z₀$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = R₀$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ + jX₀$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\sqrt{\frac{r}{g}}$ = $\sqrt{\frac{l}{c}}$ = R₀ è solo resistiva ed indipendente dalla frequenza, rendendo semplice realizzare la condizione di adattamento Z_g$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Z_c$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = R₀, che determina al contempo anche il massimo trasferimento di potenza.

In definitiva, la funzione di trasferimento complessiva H_q$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = H_i$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$H_q$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$H_u$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ vale in questo caso H$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{1}{2}}$2e^{-d$\sqrt{rg}$}e^{-jd2$\pi$f$\sqrt{lc}$}${\frac{1}{2}}$ = ${\frac{1}{2}}$e^{-d$\sqrt{rg}$}e^{-jd2$\pi$f$\sqrt{lc}$}, equivalente quindi ad un canale perfetto con guadagno G = ${\frac{1}{2}}$e^{-d$\sqrt{rg}$} e ritardo t_R = d$\sqrt{lc}$; al contempo, l'attenuazione disponibile risulta indipendente da f e pari a

A_d$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = 1/G_d$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = e^{2d$\sqrt{rg}$}