Fattore di rumore per reti in cascata

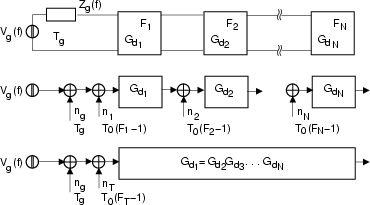
Sappiamo che il guadagno disponibile dell'unica rete due porte equivalente alle N reti poste in cascata, è pari al prodotto dei singoli guadagni, ovvero G_d = $\Pi_{n=1}^{N}$G_dn. Come determinare invece il fattore di rumore equivalente complessivo ?

0.600000

Con riferimento alla figura riportata a lato, il singolo contributo di rumore dovuto a ciascuna rete può essere riportato all'ingresso della rete stessa, individuando così una temperatura T_Qi^{$\left(\vphantom{ n}\right.$n$\left.\vphantom{ n}\right)$} = T₀$\left(\vphantom{ F^{\left( n\right) }-1}\right.$F^{$\left(\vphantom{ n}\right.$n$\left.\vphantom{ n}\right)$} - 1$\left.\vphantom{ F^{\left( n\right) }-1}\right)$. I singoli contributi possono quindi essere riportati a monte delle reti che li precedono, dividendo la potenza (ovvero la temperatura) per il guadagno disponibile delle reti ``scavalcate''. Dato che i contributi di rumore sono indipendenti, le loro potenze si sommano, e dunque è lecito sommare le singole temperature T_Qi^{$\left(\vphantom{ n}\right.$n$\left.\vphantom{ n}\right)$} riportate all'ingresso, in modo da ottenere un unico contributo complessivo di valore

T_Qi^{$\left(\vphantom{ T}\right.$T$\left.\vphantom{ T}\right)$} = T_Qi^{$\left(\vphantom{ 1}\right.$1$\left.\vphantom{ 1}\right)$} + T_Qi^{$\left(\vphantom{ 2}\right.$2$\left.\vphantom{ 2}\right)$}$${\frac{1}{G_{d_{1}}}}$$ + T_Qi^{$\left(\vphantom{ 3}\right.$3$\left.\vphantom{ 3}\right)$}$${\frac{1}{G_{d_{1}}G_{d_{2}}}}$$ + ^... + T_Qi^{$\left(\vphantom{ N}\right.$N$\left.\vphantom{ N}\right)$}$${\frac{1}{\Pi _{n=1}^{N-1}G_{d_{n}}}}$$

in cui, sostituendo le espressioni per i T_Qi^{$\left(\vphantom{ n}\right.$n$\left.\vphantom{ n}\right)$} si ottiene

T_Qi^{$\left(\vphantom{ T}\right.$T$\left.\vphantom{ T}\right)$} = T₀ ^. $$\left[\vphantom{ F_{1}-1+\frac{F_{2}-1}{G_{d_{1}}}+\frac{F_{3}-1}{G_{d_{1}}G_{d_{2}}}+\cdots +\frac{F_{N}-1}{\Pi _{n=1}^{N-1}G_{d_{n}}}}\right.$$F₁ - 1 + $${\frac{F_{2}-1}{G_{d_{1}}}}$$ + $${\frac{F_{3}-1}{G_{d_{1}}G_{d_{2}}}}$$ + ^... + $${\frac{F_{N}-1}{\Pi _{n=1}^{N-1}G_{d_{n}}}}$$ $$\left.\vphantom{ F_{1}-1+\frac{F_{2}-1}{G_{d_{1}}}+\frac{F_{3}-1}{G_{d_{1}}G_{d_{2}}}+\cdots +\frac{F_{N}-1}{\Pi _{n=1}^{N-1}G_{d_{n}}}}\right]$$

Applicando la definizione F^{$\left(\vphantom{ T}\right.$T$\left.\vphantom{ T}\right)$} = 1 + ${\frac{T^{\left( T\right) }_{Q_{i}}}{T_{0}}}$, si ottiene

F^{$\left(\vphantom{ T}\right.$T$\left.\vphantom{ T}\right)$} = F₁ + $${\frac{F_{2}-1}{G_{d_{1}}}}$$ + $${\frac{F_{3}-1}{G_{d_{1}}G_{d_{2}}}}$$ + ^... + $${\frac{F_{N}-1}{\Pi _{n=1}^{N-1}G_{d_{n}}}}$$

che costituisce proprio l'espressione cercata:

F^{$\left(\vphantom{ T}\right.$T$\left.\vphantom{ T}\right)$} = F₁ + $$\sum_{i=2}^{N}$$$${\frac{F_{i}-1}{\Pi _{j=1}^{i-1}G_{d_{j}}}}$$

Il risultato si presta alle seguenti considerazioni:

• La prima rete due porte deve avere un F più piccolo possibile, in quanto quest'ultimo non può essere ridotto in alcun modo e contribuisce per intero ad F^{$\left(\vphantom{ T}\right.$T$\left.\vphantom{ T}\right)$};
• la prima rete deve avere G_d più elevato possibile, in quanto quest'ultimo divide tutti i contributi di rumore delle reti seguenti.

Pertanto l'elemento che determina in modo preponderante il rumore prodotto da una cascata di reti due porte è la prima rete della serie, ed il suo progetto deve essere eseguito con cura particolare, anche tenendo conto del fatto che le due esigenze sopra riportate sono spesso in contrasto tra loro. E' inoltre appena il caso di ricordare che l'espressione ottenuta non è in dB, mentre spesso F è fornito appunto in dB; pertanto per il calcolo di F^{$\left(\vphantom{ T}\right.$T$\left.\vphantom{ T}\right)$} occorre prima esprimere tutti gli F_i in unità lineari.

Esercizio

 

0.350000

 Una trasmissione video con portante f_p = 2 GHz viene ricevuta secondo uno dei due schemi in figura, indicati come caso A e B. E' presente una discesa in cavo coassiale con $\phi$ = 1.2/4.4 mm lunga 50 metri, un filtro-amplificatore con guadagno disponibile G_d1 = 20 dB, fattore di rumore F = 2 dB e banda di rumore B_N = 7 MHz, ed un mixer che converte il segnale a frequenza intermedia f_I, e che esibisce G_d2 = 0 dB e F₂ = 10 dB. Tutti i componenti a valle dell'antenna si trovano alla stessa temperatura T₀ = 290 ^oK. Calcolare:

1)

La minima potenza disponibile W_dR che occorre ricevere per ottenere SNR₀ = 50 dB nei due casi. Ripetere il calcolo supponendo l'antenna ricevente a temperatura T_a = 10 ^oK anziché T₀.

2)

La minima potenza che è necessario trasmettere per superare un collegamento terrestre lungo 50 Km, con antenne di guadagno G_T = G_R = 30 dB. Ripetere il calcolo per un down link satellitare in orbita geostazionaria.

3)

Il valore efficace della tensione ai capi del generatore equivalente di uscita dell'amplificatore di potenza del trasmettitore, per il caso migliore (tra A e B) del collegamento terrestre, nel caso di massimo trasferimento di potenza con Z_u = Z_a = 50 $\Omega$, oppure con Z_u = 50 $\Omega$ e Z_a = 50 - j 50 $\Omega$.

Svolgimento

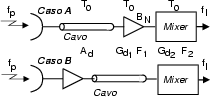
Determiniamo innanzitutto l'attenuazione del cavo coassiale, che risulta A_d$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = A₀$\sqrt{f\left( MHz\right) }$ dB/Km. Per il diametro indicato risulta A₀ = 5.3 dB/Km, ed alla frequenza di 2 GHz si ottiene A_d$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)_{dB}^{}$ = 5.3$\sqrt{2\cdot 10^{3}}$ = 237 dB/Km; e quindi in 50 metri si ha 11.85 $\simeq$ 12 dB. Riassumendo:

	Ad	F1	Gd1	F2	Gd2
dB	12	2	20	10	0
lineare	15.8	1.6	100	10	1

<><>

1)

 

A)

Il fattore di rumore complessivo risulta

    F_A = F_coax + A_d$\left(\vphantom{ F_{1}-1}\right.$F₁ - 1$\left.\vphantom{ F_{1}-1}\right)$ + ${\frac{A_{d}}{G_{d_{1}}}}$$\left(\vphantom{ F_{2}-1}\right.$F₂ - 1$\left.\vphantom{ F_{2}-1}\right)$ = 26.7   $\rightarrow$  14.3 dB.

Dato che per la trasmissione televisiva AM-BLU risulta SNR = SNR₀, scriviamo

     W_dR = SNR_i ^. W_dN = SNR₀ ^. F_A ^. B_N ^. kT₀ e quindi

    W_dR(dBm) = SNR₀(dB) + F_A(dB) + B_N(dBMHz) + KT₀(dBm/MHz) =

                      = 50 + 14.3 + 8.45 - 114 = -41.25 dBm

B)

Il fattore di rumore complessivo risulta ora

    F_B

= F₁ + ${\frac{\left( F_{coax}-1\right) }{G_{d_{1}}}}$ + ${\frac{A_{d}}{G_{d_{1}}}}$$\left(\vphantom{ F_{2}-1}\right.$F₂ - 1$\left.\vphantom{ F_{2}-1}\right)$ = 3.17   $\rightarrow$  5 dB.

La differenza con il caso A è di 9.3 dB, e la potenza disponibile che occorre ricevere diminuisce pertanto della stessa quantità, e quindi ora risulta W_dR = -50.55 dBm.

Nel caso in cui T_a = 10 ^oK $\neq$ T₀, non si ottiene più T_ei = FT₀, ma occorre introdurre la T_Qi della rete riportata al suo ingresso, e considerare la rete non rumorosa in modo da scrivere T_ei = T_g + T_Qi = T_A + T₀$\left(\vphantom{ F-1}\right.$F - 1$\left.\vphantom{ F-1}\right)$. Ripetiamo i calcoli per i due casi A e B:

A)

W_dR = SNR ^. W_dN = SNR ^. B_N ^. k ^. $\left(\vphantom{ T_{a}+T_{Q_{i}}}\right.$T_a + T_Qi$\left.\vphantom{ T_{a}+T_{Q_{i}}}\right)$ = SNR ^. B_N ^. k ^. $\left(\vphantom{ T_{a}+T_{0}\left( F_{A}-1\right) }\right.$T_a + T₀$\left(\vphantom{ F_{A}-1}\right.$F_A - 1$\left.\vphantom{ F_{A}-1}\right)$ $\left.\vphantom{ T_{a}+T_{0}\left( F_{A}-1\right) }\right)$;

W_dR(dBW) = SNR(dB) + 10log₁₀7 ^. 10⁺⁶ + 10log₁₀$\left(\vphantom{ 1.38\cdot 10^{-23}\left( 10+290\cdot 25.7\right) }\right.$1.38 ^. 10^-23$\left(\vphantom{ 10+290\cdot 25.7}\right.$10 + 290 ^. 25.7$\left.\vphantom{ 10+290\cdot 25.7}\right)$ $\left.\vphantom{ 1.38\cdot 10^{-23}\left( 10+290\cdot 25.7\right) }\right)$ =

                           = 50 + 68.5 - 190 = -71.5 dBW = -41.5 dBm

B)

W_dR(dBW) = 50 + 68.5 - 10log₁₀$\left(\vphantom{ 1.38\cdot 10^{-23}\left( 10+290\cdot 2.17\right) }\right.$1.38 ^. 10^-23$\left(\vphantom{ 10+290\cdot 2.17}\right.$10 + 290 ^. 2.17$\left.\vphantom{ 10+290\cdot 2.17}\right)$ $\left.\vphantom{ 1.38\cdot 10^{-23}\left( 10+290\cdot 2.17\right) }\right)$ = - 82 dBW = -52 dBm

Notiamo che se la T_a è ridotta, le prestazioni per la configurazione A migliorano di soli 0.25 dB, mentre nel caso B il miglioramento è di circa 1.5 dB. Questo risultato trova spiegazione con il fatto che in A predomina comunque il T_Qi prodotto dal cavo.

2)

In un collegamento radio terrestre si assume T_a = 290 ^oK. Inoltre, per il caso in esame si trova una attenuazione disponibile pari a

A_d = 32.4 + 20log₁₀f(MHz) + 20log₁₀d(Km) - G_T - G_R = 32.4 + 66 + 34 - 60 =

     = 72.4 dB

A)

W_dT = W_dR + A_d = - 41.25 + 72.4 = 31.15 dBm = 1.15 dBW $\rightarrow$ 1.3 Watt

B)

W_dT = W_dR + A_d = - 50.55 + 72.4 = 21.85 dBm = - 8.15 dBW $\rightarrow$ 153.1 mWatt

Per

il downlink si ha d = 36.000 Km, mentre T_a = 10 ^oK. Pertanto:

    A_d = 32.4 + 20log₁₀f(MHz) + 20log₁₀d(Km) - G_T - G_R = 32.4 + 66 + 91.12 - 60

         = 129.5 dB

e quindi, utilizzando il valore W_dR ottenuto per il caso B, otteniamo

     W_dT = W_dR + A_d = - 52 + 129.5 = 77.5 dBm = 47.5 dBW $\rightarrow$ 56.2 KWatt

3)

Nel caso di adattamento, la potenza ceduta all'antenna T_x è proprio quella disponibile del generatore, e quindi si ha W_dT = ${\frac{\sigma _{g}^{2}}{4R}}$, da cui

     $\sigma_{g}^{}$ = $\sqrt{W_{d_{T}}4R}$ = $\sqrt{153\cdot 10^{-3}\cdot 4\cdot 50}$ = 5.53 Volt.

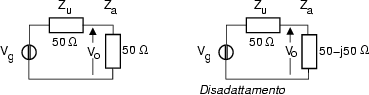
In caso di disadattamento, desiderando che la potenza ceduta all'antenna trasmittente rimanga la stessa, e supponendo le impedenze indipendenti dalla frequenza, scriviamo (in accordo alla relazione mostrata in (12.1))

     $\mathcal {W}$_T = $\mathcal {P}$_vo${\frac{R_{a}}{\left\vert Z_{a}\right\vert ^{2}}}$ = P_vo${\frac{50}{50^{2}+50^{2}}}$ = P_vo ^. 10^-2

e quindi P_vo $\simeq$ 15.3 (Volt²). Applicando ora la regola del partitore, si ottiene

     P_vo = P_vg$\left\vert\vphantom{ \frac{Z_{a}}{Z_{a}+Z_{u}}}\right.$${\frac{Z_{a}}{Z_{a}+Z_{u}}}$ $\left.\vphantom{ \frac{Z_{a}}{Z_{a}+Z_{u}}}\right\vert^{2}_{}$ = P_vg$\left\vert\vphantom{ \frac{50-j50}{50+50-j50}}\right.$${\frac{50-j50}{50+50-j50}}$ $\left.\vphantom{ \frac{50-j50}{50+50-j50}}\right\vert^{2}_{}$ = P_vg${\frac{50^{2}+50^{2}}{100^{2}+50^{2}}}$ = P_vg ^. 0.4.

Dunque, P_vg = ${\frac{P_{v_{o}}}{0.4}}$ = ${\frac{15.5}{0.4}}$ = 38.75 Volt², ovvero V_geff = $\sqrt{38.75}$ = 6.225 Volt.

Evidentemente, il disadattamento produce un innalzamento del valore efficace, se si vuol mantenere la stessa potenza di uscita.

              

Esercizio

Un trasmettitore con potenza di 50 mW e portante 30 MHz, modula AM un segnale con banda $\pm$W = $\pm$ 10 KHz. Qualora si desideri mantenere un SNR in ricezione di almeno 25 dB, determinare la distanza che è possibile coprire adottando antenne isotrope, ed un ricevitore caratterizzato da un fattore di rumore F = 10 dB.

Svolgimento

Assumendo che la trasmissione sia BLD-PS e che si verifichino le condizioni di massimo trasferimento di potenza, la potenza che è necessario ricevere può essere determinata come $\mathcal {W}$_R = W ^. N₀ ^. SNR = B ^. kT₀F ^. SNR, e quindi

       $\mathcal {W}$_R(dBm) = 40 - 174(dBm/Hz) + 10 + 25 = -99 dBm.

Il guadagno di sistema risulta allora pari a

      G_s(dB) = $\mathcal {W}$_T(dBm) - $\mathcal {W}$_R(dBm) = 10 log₁₀50 + 99 = 17 + 99 = 116 dB.

Non prevedendo nessun margine, l'attenuazione dovuta alla distanza è numericamente pari al guadagno di sistema, e pertanto scriviamo

      116 = 32.4 + 20 log₁₀f(MHz) + 20 log₁₀d(Km) = 32.4 + 29.5 + 20 log₁₀d(Km)

e quindi 2.7 = log₁₀d(Km), da cui d = 10^2.7 = 501 Km.

Svolgendo nuovamente i calcoli nel caso in cui il fattore di rumore del ricevitore sia pari a 20 dB e 100 dB, si ottiene che la nuova massima distanza risulta rispettivamente di 158 Km e di 15 metri.