Avanti: Integrale di convoluzione
Su: Risposta Impulsiva e Convoluzione
Indietro: Risposta Impulsiva e Convoluzione
Indice
Indice analitico
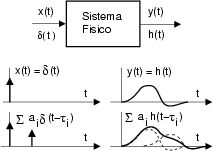
Consideriamo un sistema fisico (elettrico, meccanico, pneumatico...) che venga
sollecitato (in un punto considerato come ingresso) da un segnale impulsivo
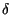
 t
t , e consideriamo l'andamento temporale di una
grandezza (meccanica, pneumatica, elettrica...) che possiamo considerare una
uscita. Tale risultato prende il nome di risposta impulsiva (ossia all'impulso)
e viene indicata con
h
, e consideriamo l'andamento temporale di una
grandezza (meccanica, pneumatica, elettrica...) che possiamo considerare una
uscita. Tale risultato prende il nome di risposta impulsiva (ossia all'impulso)
e viene indicata con
h t
t . L'andamento di
h
. L'andamento di
h t
t rappresenta la grandezza di uscita, osservata dopo che è passato un tempo pari
a t da quando si è applicato in ingresso l'impulso
rappresenta la grandezza di uscita, osservata dopo che è passato un tempo pari
a t da quando si è applicato in ingresso l'impulso
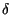
 t
t .
.
Se il sistema è lineare e permanente3.9, applicando un ingresso costituito da più impulsi, ognuno con area differente
ai e centrato ad un diverso istante 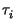 , ovvero
si ottiene una uscita pari a
Si rifletta sul significato della sommatoria, con l'aiuto della figura a lato:
ad un dato istante t, il valore dell'uscita
y
, ovvero
si ottiene una uscita pari a
Si rifletta sul significato della sommatoria, con l'aiuto della figura a lato:
ad un dato istante t, il valore dell'uscita
y t
t risulta dalla somma di N termini, ognuno pari al valore della risposta
impulsiva calcolata con argomento pari alla differenza tra istante di osservazione
ed istante di applicazione dell'i-esimo impulso.
risulta dalla somma di N termini, ognuno pari al valore della risposta
impulsiva calcolata con argomento pari alla differenza tra istante di osservazione
ed istante di applicazione dell'i-esimo impulso.





Avanti: Integrale di convoluzione
Su: Risposta Impulsiva e Convoluzione
Indietro: Risposta Impulsiva e Convoluzione
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]()
![]() t
t![]() , e consideriamo l'andamento temporale di una
grandezza (meccanica, pneumatica, elettrica...) che possiamo considerare una
uscita. Tale risultato prende il nome di risposta impulsiva (ossia all'impulso)
e viene indicata con
h
, e consideriamo l'andamento temporale di una
grandezza (meccanica, pneumatica, elettrica...) che possiamo considerare una
uscita. Tale risultato prende il nome di risposta impulsiva (ossia all'impulso)
e viene indicata con
h![]() t
t![]() . L'andamento di
h
. L'andamento di
h![]() t
t![]() rappresenta la grandezza di uscita, osservata dopo che è passato un tempo pari
a t da quando si è applicato in ingresso l'impulso
rappresenta la grandezza di uscita, osservata dopo che è passato un tempo pari
a t da quando si è applicato in ingresso l'impulso
![]()
![]() t
t![]() .
.