




Avanti: ht come funzione memoria
Su: Risposta Impulsiva e Convoluzione
Indietro: Risposta Impulsiva
Indice
Indice analitico
Consideriamo ancora lo stesso sistema fisico, al cui ingresso sia posto un generico
segnale
x t
t che, grazie alla proprietà di setacciamento,
rappresentiamo come scomposto in infiniti termini, ossia come somma integrale
di impulsi centrati in
che, grazie alla proprietà di setacciamento,
rappresentiamo come scomposto in infiniti termini, ossia come somma integrale
di impulsi centrati in  (variabile) ed area
x
(variabile) ed area
x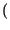

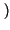 d
d (infinitesima):
(infinitesima):
Questa espressione, formalmente simile alla (3.1), è equivalente
alla proprietà di setacciamento, dato che
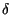
 t
t è una
funzione pari. L'andamento della grandezza di uscita sarà il risultato della
sovrapposizione di infinite risposte impulsive, ognuna relativa ad un diverso
valore dell'ingresso:
in cui
x
è una
funzione pari. L'andamento della grandezza di uscita sarà il risultato della
sovrapposizione di infinite risposte impulsive, ognuna relativa ad un diverso
valore dell'ingresso:
in cui
x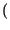

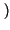 d
d è l'area degli impulsi che costituiscono
l'ingresso, e
h
è l'area degli impulsi che costituiscono
l'ingresso, e
h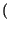 t -
t - 
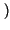 è l'uscita all'istante t
causata dall'impulso in ingresso centrato all'istante
è l'uscita all'istante t
causata dall'impulso in ingresso centrato all'istante  . Il risultato
ottenuto, formalmente simile a (3.2), prende il nome di integrale
di convoluzione, viene indicato in forma simbolica da un asterisco (*),
e gode della proprietà commutativa, ovvero
. Il risultato
ottenuto, formalmente simile a (3.2), prende il nome di integrale
di convoluzione, viene indicato in forma simbolica da un asterisco (*),
e gode della proprietà commutativa, ovvero
y t
t = x
= x t
t *h
*h t
t =
=
= 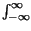 x
x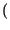

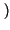 h
h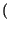 t -
t - 
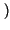 d
d =
= 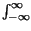 h
h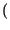

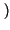 x
x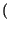 t -
t - 
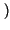 d
d
La notazione con l'asterisco fa sì che ci si riferisca ad essa come
al ``prodotto di convoluzione''. Notiamo come
h t
t caratterizzi
completamente il sistema fisico, in quanto permette di calcolarne l'uscita per
un qualsiasi ingresso.
caratterizzi
completamente il sistema fisico, in quanto permette di calcolarne l'uscita per
un qualsiasi ingresso.





Avanti: ht come funzione memoria
Su: Risposta Impulsiva e Convoluzione
Indietro: Risposta Impulsiva
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() t
t![]() che, grazie alla proprietà di setacciamento,
rappresentiamo come scomposto in infiniti termini, ossia come somma integrale
di impulsi centrati in
che, grazie alla proprietà di setacciamento,
rappresentiamo come scomposto in infiniti termini, ossia come somma integrale
di impulsi centrati in ![]() (variabile) ed area
x
(variabile) ed area
x![]()
![]()
![]() d
d![]() (infinitesima):
(infinitesima):

![]() t
t![]() = x
= x![]() t
t![]() *h
*h![]() t
t![]() =
=
![]() x
x![]()
![]()
![]() h
h![]() t -
t - ![]()
![]() d
d![]() =
= ![]() h
h![]()
![]()
![]() x
x![]() t -
t - ![]()
![]() d
d![]()
![]() t
t![]() caratterizzi
completamente il sistema fisico, in quanto permette di calcolarne l'uscita per
un qualsiasi ingresso.
caratterizzi
completamente il sistema fisico, in quanto permette di calcolarne l'uscita per
un qualsiasi ingresso.