Avanti: Medie, Momenti e Momenti Centrati
Su: Variabili aleatorie
Indietro: Variabili aleatorie
Indice
Indice analitico
CosÝ come un oggetto non omogeneo Ŕ pi˙ o meno denso in regioni differenti del
suo volume complessivo, cosÝ la densitÓ di probabilitÓ mostra su quali
valori della variabile aleatoria si concentra la probabilitÓ. CosÝ, ad esempio,
la densitÓ della v.a. discreta associata al lancio di un dado pu˛ essere scritta:
pD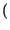 x
x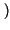 =
= 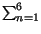
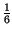
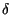
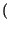 x - n
x - n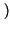 il cui significato discutiamo subito, con l'aiuto dei due grafici seguenti.
il cui significato discutiamo subito, con l'aiuto dei due grafici seguenti.
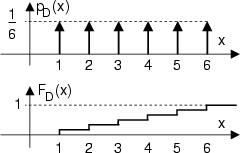
D e x indicano rispettivamente la v.a. (il numero che uscirÓ)
ed una sua realizzazione (una delle 6 facce). I 6 impulsi centrati in x = n
rappresentano una concentrazione di probabilitÓ nei sei possibili valori; l'area
di tali impulsi Ŕ proprio pari alla probabilitÓ di ognuno dei sei risultati.
E' facile verificare che
e che risulta
ovvero pari alla probabilitÓ che la v.a. D assuma un valore tra a
e b. In particolare, non potendosi verificare una probabilitÓ negativa,
si ha
pD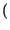 x
x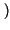
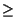 0 con
0 con 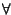 x.
x.
Una funzione di v.a. strettamente collegata alla densitÓ Ŕ la funzione distribuzione
di probabilitÓ5.7, definita come
che risulta una funzione non decrescente di x, limitata ad un massimo
valore di 1, ed il cui andamento mostriamo sotto alla
pD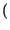 x
x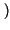 ,
nel caso dell'esempio del lancio del dado5.8.
,
nel caso dell'esempio del lancio del dado5.8.
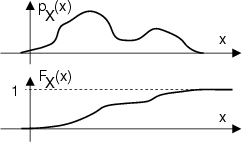
Le definizioni date mantengono validitÓ nel caso di v.a. continua, originando
le curve mostrate nei due grafici a lato. Ora Ŕ ancora pi˙ evidente la circostanza
che
pX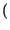 x
x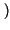 Ŕ una densitÓ, e diviene una probabilitÓ
solo quando moltiplicata per un intervallo di x(5.9).
Ŕ una densitÓ, e diviene una probabilitÓ
solo quando moltiplicata per un intervallo di x(5.9).
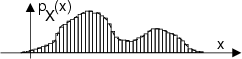
Per finire, citiamo la stretta relazione che intercorre tra la densitÓ di probabilitÓ
e l'istogramma. Quest'ultimo pu˛ essere realizzato se sono disponibili
serie di realizzazioni della v.a., e si ottiene suddividendo il campo di variabilitÓ
della grandezza X in sotto-intervalli, e disegnando rettangoli verticali,
ognuno di altezza pari al numero di volte che (nel'ambito del campione statistico
a disposizione) X assume un valore in quell'intervallo. Dividendo l'altezza
di ogni rettangolo per il numero di osservazioni N, si ottiene una approssimazione
di
pX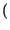 x
x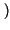 , via via pi˙ precisa con
N
, via via pi˙ precisa con
N 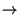
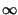 ,
e con una conseguente riduzione dell'estensione degli intervalli.
,
e con una conseguente riduzione dell'estensione degli intervalli.





Avanti: Medie, Momenti e Momenti Centrati
Su: Variabili aleatorie
Indietro: Variabili aleatorie
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() x
x![]() =
= ![]()
![]()
![]()
![]() x - n
x - n![]() il cui significato discutiamo subito, con l'aiuto dei due grafici seguenti.
il cui significato discutiamo subito, con l'aiuto dei due grafici seguenti.
![]() x
x![]() Ŕ una densitÓ, e diviene una probabilitÓ
solo quando moltiplicata per un intervallo di x(5.9).
Ŕ una densitÓ, e diviene una probabilitÓ
solo quando moltiplicata per un intervallo di x(5.9).