



Avanti: Stima spettrale
Su: Densità Spettrale
Indietro: Teorema di Wiener
Indice
Indice analitico
E' definito in base ad una sua generica realizzazione
che, se il parametro 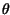 è una variabile aleatoria uniformemente
distribuita tra -
è una variabile aleatoria uniformemente
distribuita tra - 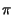 e -
e - 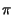 (ossia
p
(ossia
p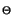
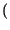
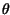
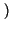 =
= 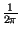 rect2
rect2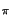
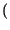
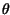
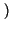 ),
descrive un processo ergodico.
),
descrive un processo ergodico.
Sappiamo che una sua realizzazione (ad esempio quella con 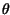 = 0)
ha una densità di potenza
= 0)
ha una densità di potenza
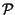 x
x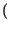 f
f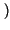 =
= 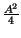
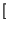
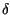
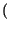 f - f0
f - f0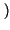 +
+ 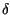
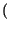 f + f0
f + f0
![$ \left.\vphantom{ \delta \left( f-f_{0}\right) +\delta \left( f+f_{0}\right) }\right]$](img1959.gif) .
Possiamo quindi ottenere l'autocorrelazione
.
Possiamo quindi ottenere l'autocorrelazione
senza dover svolgere l'integrale:
Il risultato trovato conferma che l'autocorrelazione di un segnale periodico
è periodica; riflettiamo dunque sulla circostanza che anche un seno, od un coseno
con qualunque altra fase, avrebbe avuto la stessa
 x
x t
t .
Ciò è d'altra parte evidente, avendo tutti questi segnali uguali densità
.
Ciò è d'altra parte evidente, avendo tutti questi segnali uguali densità
 x
x f
f .
.
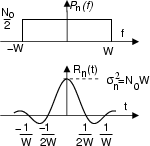
Il processo
n t
t è chiamato bianco perché costante
in frequenza, e descritto da una densità di potenza pari a
è chiamato bianco perché costante
in frequenza, e descritto da una densità di potenza pari a
in cui W è l'occupazione di banda a frequenze positive. In tali ipotesi
otteniamo
In particolare, campioni presi a distanza
Tc = 1/2W sono incorrelati
(ed essendo il processo gaussiano anche statisticamente indipendenti); questo
risultato giustifica, almeno da un punto di vista teorico, una ipotesi che viene
spesso fatta: quella di trovare sovrapposti ai campioni di segnale, dei campioni
di rumore statisticamente indipendenti.
All'aumentare di W,
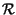 n
n t
t tende a zero
più rapidamente, cosicchè il rumore si mantiene correlato per un tempo sempre
minore, ovvero due campioni estratti ad una stessa distanza t hanno una
correlazione sempre minore. Un risultato simile vale anche più in generale,
in quanto l'autocorrelazione
tende a zero
più rapidamente, cosicchè il rumore si mantiene correlato per un tempo sempre
minore, ovvero due campioni estratti ad una stessa distanza t hanno una
correlazione sempre minore. Un risultato simile vale anche più in generale,
in quanto l'autocorrelazione
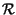 x
x t
t di un qualsiasi
processo (tranne nel caso periodico, riconducibile ad una combinazione di processi
armonici) tende a 0 con
t
di un qualsiasi
processo (tranne nel caso periodico, riconducibile ad una combinazione di processi
armonici) tende a 0 con
t 
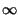 , ovvero da un certo t
in poi la correlazione è trascurabile.
, ovvero da un certo t
in poi la correlazione è trascurabile.
Abbiamo già descritto un generico segnale numerico
come una somma di repliche di una funzione
g t
t , con ampiezze
an rappresentative dei valori da trasmettere:
, con ampiezze
an rappresentative dei valori da trasmettere:
La presenza della variabile aleatoria 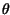 a distribuzione uniforme
tra
a distribuzione uniforme
tra
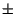
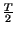 (per cui
p
(per cui
p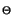
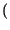
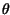
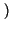 =
= 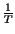 rectT
rectT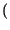
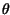
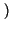 ),
rende
x
),
rende
x t
t un processo ergodico.
un processo ergodico.
Si mostrerà in appendice 7.9.2 che, nelle ipotesi in cui
le ampiezze an siano determinazioni di variabili aleatorie indipendenti
ed identicamente distribuite, a media nulla e varianza
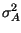 ,
l'autocorrelazione di
x
,
l'autocorrelazione di
x t
t vale
vale
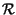 x
x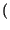
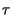
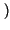 =
= 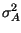
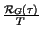 in cui
in cui
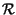 G
G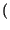
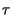
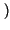 è l'autocorrelazione di
g
è l'autocorrelazione di
g t
t ,
e dunque
,
e dunque
Osserviamo innanzitutto che è per questa via che si sono caratterizzate le densità
di potenza proprie dei codici di linea. Limitandoci a voler interpretare il
risultato, notiamo che
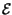 G
G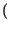 f
f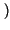 è la densità di
energia di una singola replica di
g
è la densità di
energia di una singola replica di
g t
t . La sua ripetizione,
con periodo T, fornisce una densità di potenza media
. La sua ripetizione,
con periodo T, fornisce una densità di potenza media
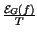 .
Se ogni replica di
g
.
Se ogni replica di
g t
t è moltiplicata per una v.a. indipendente
a media nulla e varianza (potenza)
è moltiplicata per una v.a. indipendente
a media nulla e varianza (potenza)
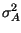 , la densità di potenza
, la densità di potenza
 x
x f
f aumenta di egual misura. Un'ultima avvertenza
riguarda il fatto che, se gli an non sono indipendenti, il risultato
è più complesso (vedi appendice 7.9.2).
aumenta di egual misura. Un'ultima avvertenza
riguarda il fatto che, se gli an non sono indipendenti, il risultato
è più complesso (vedi appendice 7.9.2).
Sottosezioni




Avanti: Stima spettrale
Su: Densità Spettrale
Indietro: Teorema di Wiener
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() è una variabile aleatoria uniformemente
distribuita tra -
è una variabile aleatoria uniformemente
distribuita tra - ![]() e -
e - ![]() (ossia
p
(ossia
p![]()
![]()
![]()
![]() =
= ![]() rect2
rect2![]()
![]()
![]()
![]() ),
descrive un processo ergodico.
),
descrive un processo ergodico.
![]() = 0)
ha una densità di potenza
= 0)
ha una densità di potenza
![]() x
x![]() f
f![]() =
= ![]()
![]()
![]()
![]() f - f0
f - f0![]() +
+ ![]()
![]() f + f0
f + f0![]()
![]() .
Possiamo quindi ottenere l'autocorrelazione
.
Possiamo quindi ottenere l'autocorrelazione
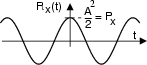
![]() t
t![]() è chiamato bianco perché costante
in frequenza, e descritto da una densità di potenza pari a
è chiamato bianco perché costante
in frequenza, e descritto da una densità di potenza pari a
![]() n
n![]() t
t![]() tende a zero
più rapidamente, cosicchè il rumore si mantiene correlato per un tempo sempre
minore, ovvero due campioni estratti ad una stessa distanza t hanno una
correlazione sempre minore. Un risultato simile vale anche più in generale,
in quanto l'autocorrelazione
tende a zero
più rapidamente, cosicchè il rumore si mantiene correlato per un tempo sempre
minore, ovvero due campioni estratti ad una stessa distanza t hanno una
correlazione sempre minore. Un risultato simile vale anche più in generale,
in quanto l'autocorrelazione
![]() x
x![]() t
t![]() di un qualsiasi
processo (tranne nel caso periodico, riconducibile ad una combinazione di processi
armonici) tende a 0 con
t
di un qualsiasi
processo (tranne nel caso periodico, riconducibile ad una combinazione di processi
armonici) tende a 0 con
t ![]()
![]() , ovvero da un certo t
in poi la correlazione è trascurabile.
, ovvero da un certo t
in poi la correlazione è trascurabile.
![]() t
t![]() , con ampiezze
an rappresentative dei valori da trasmettere:
, con ampiezze
an rappresentative dei valori da trasmettere:
![]() ,
l'autocorrelazione di
x
,
l'autocorrelazione di
x![]() t
t![]() vale
vale
![]() x
x![]()
![]()
![]() =
= ![]()
![]() in cui
in cui
![]() G
G![]()
![]()
![]() è l'autocorrelazione di
g
è l'autocorrelazione di
g![]() t
t![]() ,
e dunque
,
e dunque