Trasmissione a banda laterale unica

Consideriamo un segnale a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ reale e limitato in banda, con A$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = A^*$\left(\vphantom{ -f}\right.$ - f$\left.\vphantom{ -f}\right)$ (grafico [A]), a simmetria coniugata. Come già illustrato, la conoscenza di A⁺$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = A$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$rect_W$\left(\vphantom{ f-\frac{W}{2}}\right.$f - ${\frac{W}{2}}$ $\left.\vphantom{ f-\frac{W}{2}}\right)$ è sufficiente a definire a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ in modo completo, in virtù della simmetria coniugata. Se definiamo x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$cos$\omega_{0}^{}$t, anch'esso reale, otteniamo che X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ [B], oltre ad essere a simmetria coniugata rispetto all'origine, ha simmetria coniugata anche rispetto ad f₀: X⁺$\left(\vphantom{ f+f_{0}}\right.$f + f₀$\left.\vphantom{ f+f_{0}}\right)$ = $\left\{\vphantom{ X^{+}\left( -f+f_{0}\right) }\right.$X⁺$\left(\vphantom{ -f+f_{0}}\right.$ - f + f₀$\left.\vphantom{ -f+f_{0}}\right)$ $\left.\vphantom{ X^{+}\left( -f+f_{0}\right) }\right\}^{*}_{}$ [C].

 

0.400000

Questo risultato mostra come sia teoricamente possibile (con una fotocopiatrice ed un paio di forbici!) ottenere il segnale X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ a partire da un Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ [D], con Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ ottenuta da X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ eliminandone metà banda. La ricostruzione di X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ avviene infatti (frecce tratteggiate) spostando le copie duplicate di Y⁺$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ e Y^-$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ come indicato dalle frecce.

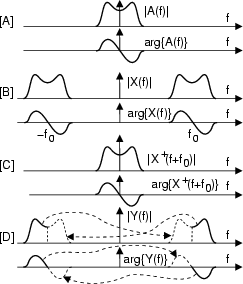
Una volta verificata l'esattezza del procedimento illustrato, che ci consente di ricevere per intero X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ trasmettendone solo metà (cioè Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$), osserviamo che anche Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ è a simmetria coniugata rispetto a zero (ossia Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = Y^*$\left(\vphantom{ -f}\right.$ - f$\left.\vphantom{ -f}\right)$), e quindi la sua antitrasformata y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ è reale, e dunque può essere realmente trasmesso.

A parte il ``dettaglio'' di come ricostruire ``veramente'' X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ a partire da Y$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$, ci chiediamo: esiste una formula per ottenere y$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ in modo diretto a partire da a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$? La risposta è positiva; per provarla occorre però affrontare alcune pagine di teoria, che illustrano un metodo di rappresentazione (nel dominio del tempo) per segnali modulati.