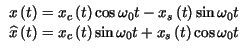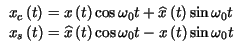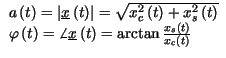Avanti: Segnale Analitico
Su: Rappresentazione dei segnali modulati
Indietro: Componenti analogiche di bassa frequenza
Indice
Indice analitico
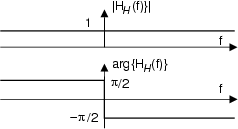
Il filtro di Hilbert è definito da una risposta in frequenza
ed in in figura è mostrato l'andamento costante del modulo
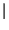 H
H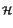
 f
f
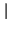 = 1,
e quello della fase
= 1,
e quello della fase
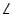 H
H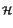
 f
f che passa
da
che passa
da
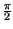 per f < 0 a
-
per f < 0 a
- 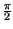 per f > 0.
Il risultato del passaggio di un segnale
x
per f > 0.
Il risultato del passaggio di un segnale
x t
t attraverso8.11
attraverso8.11
il filtro di Hilbert è un un secondo segnale, identificato con la
trasformata di Hilbert del primo, indicato come
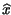
 t
t =
= 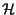
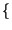 x
x t
t
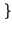 ,
ed il cui andamento in frequenza ha espressione
,
ed il cui andamento in frequenza ha espressione
ossia differisce da
X f
f per uno sfasamento di
per uno sfasamento di
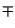
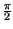 per frequenze rispettivamente positive o negative.
per frequenze rispettivamente positive o negative.
Senza soffermarci ora sulle proprietà8.12 della trasformata di Hilbert, forniamo direttamente un risultato8.13 necessario per proseguire:
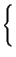
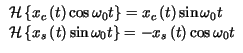 che ci permette di esprimere la trasformata di Hilbert di un segnale modulato.
Quest'ultima, assieme all'espressione di
x
che ci permette di esprimere la trasformata di Hilbert di un segnale modulato.
Quest'ultima, assieme all'espressione di
x t
t in funzione
di
xc
in funzione
di
xc t
t ed
xs
ed
xs t
t , costituisce
un sistema di due equazione in due incognite:
, costituisce
un sistema di due equazione in due incognite:
Il sistema può essere risolto8.14, permettendo in definitiva di esprimere le componenti analogiche di bassa frequenza
in termini di
x t
t e di
e di
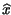
 t
t :
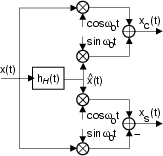
Pertanto le componenti analogiche di bassa frequenza possono essere estratte
direttamente da
x
:
Pertanto le componenti analogiche di bassa frequenza possono essere estratte
direttamente da
x t
t , utilizzando un filtro di Hilbert per
ottenere
, utilizzando un filtro di Hilbert per
ottenere
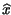
 t
t , e combinando i due segnali per
mezzo di oscillatori in quadratura. Infine,
xc
, e combinando i due segnali per
mezzo di oscillatori in quadratura. Infine,
xc t
t e
xs
e
xs t
t permettono di risalire alle modulazioni di ampiezza ed angolare:
Prima di procedere a calcolare
permettono di risalire alle modulazioni di ampiezza ed angolare:
Prima di procedere a calcolare

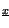
 f
f ,
occorre introdurre l'ulteriore concetto di segnale analitico.
,
occorre introdurre l'ulteriore concetto di segnale analitico.





Avanti: Segnale Analitico
Su: Rappresentazione dei segnali modulati
Indietro: Componenti analogiche di bassa frequenza
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01

![]()
![]() t
t![]() =
= ![]()
![]() x
x![]() t
t![]()
![]() ,
ed il cui andamento in frequenza ha espressione
,
ed il cui andamento in frequenza ha espressione
![]()
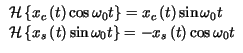 che ci permette di esprimere la trasformata di Hilbert di un segnale modulato.
Quest'ultima, assieme all'espressione di
x
che ci permette di esprimere la trasformata di Hilbert di un segnale modulato.
Quest'ultima, assieme all'espressione di
x![]() t
t![]() in funzione
di
xc
in funzione
di
xc![]() t
t![]() ed
xs
ed
xs![]() t
t![]() , costituisce
un sistema di due equazione in due incognite:
, costituisce
un sistema di due equazione in due incognite: