Data la rilevanza dei segnali con inviluppo complesso ad una sola componente, determiniamo quali condizioni si debbano verificare per dar luogo ad una simile circostanza, iniziando da un esempio.
E' descritto da una risposta in frequenza
H![]() f
f![]() nulla ovunque,
tranne che negli intervalli di frequenze
f0 - W
nulla ovunque,
tranne che negli intervalli di frequenze
f0 - W ![]()
![]() f
f![]()
![]() f0 + W
dove ha valore unitario.
f0 + W
dove ha valore unitario.
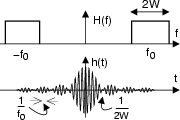
| h |
= | |
| = | 4Wsinc |
Il filtro passa banda ideale presenta
![]()
![]() t
t![]() reale,
in quanto
reale,
in quanto
![]()
![]() f
f![]() = H+
= H+![]() f + f0
f + f0![]() = rect2W
= rect2W![]() f
f![]() esibisce simmetria coniugata attorno all'origine. E' proprio questa la condizione
cercata, che ci permette di enunciare
esibisce simmetria coniugata attorno all'origine. E' proprio questa la condizione
cercata, che ci permette di enunciare
Un segnale modulato xIn altre parole,t
possiede un inviluppo complesso
t
reale, se lo spettro di quest'ultimo
f
ha simmetria coniugata attorno all'origine
f
=
- f
, ovvero il segnale analitico X+
f
ha simmetria coniugata attorno ad f0: X+
f0 +
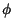
=
X+
f0 -
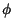
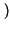
(
< W).