




Avanti: Condizioni per t reale
Su: Transito dei segnali in banda traslata
Indietro: Transito dei segnali in banda traslata
Indice
Indice analitico
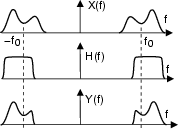
Poniamoci ora nelle condizioni generali di un segnale
x t
t che attraversa un filtro
h
che attraversa un filtro
h t
t , che per entrambi valgano
le condizioni di limitazione in banda, e che si adotti una stessa f0
di riferimento. Anche il segnale in uscita
y
, che per entrambi valgano
le condizioni di limitazione in banda, e che si adotti una stessa f0
di riferimento. Anche il segnale in uscita
y t
t è
dello stesso tipo, e come mostriamo ora, il suo inviluppo complesso risulta
è
dello stesso tipo, e come mostriamo ora, il suo inviluppo complesso risulta
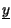
 t
t =
= 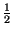
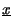
 t
t *
*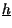
 t
t .
.
Per dimostrare il risultato, mostriamo che il segnale analitico in uscita vale
y+ t
t = x+
= x+ t
t *h+
*h+ t
t . Infatti8.19:
. Infatti8.19:
x+ t
t
*
h+ t
t
=
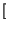 x
x*
hfp![$\displaystyle \left.\vphantom{ x*h_{fp}}\right]$](img2505.gif)
*
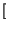 h
h*
hfp![$\displaystyle \left.\vphantom{ h*h_{fp}}\right]$](img2507.gif)
=
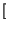 x
x*
h![$\displaystyle \left.\vphantom{ x*h}\right]$](img2509.gif)
*
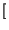 hfp
hfp*
hfp![$\displaystyle \left.\vphantom{ h_{fp}*h_{fp}}\right]$](img2511.gif)
=
y*
hfp =
y+
in cui
hfp t
t è la risposta impulsiva del filtro necessario
ad estrarre il segnale analitico. Non resta ora che mostrare lo sviluppo per
il risultato anticipato:
è la risposta impulsiva del filtro necessario
ad estrarre il segnale analitico. Non resta ora che mostrare lo sviluppo per
il risultato anticipato:
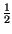 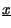  t t * *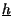  t t |
= |
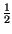 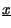  t t * *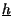  t t = = 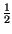 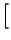 2x+ 2x+ t t e-j e-j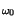 t t![$\displaystyle \left.\vphantom{ 2x^{+}\left( t\right) e^{-j\omega _{0}t}}\right]$](img2514.gif) * *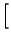 2h+ 2h+ t t e-j e-j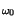 t t![$\displaystyle \left.\vphantom{ 2h^{+}\left( t\right) e^{-j\omega _{0}t}}\right]$](img2516.gif) = = |
| |
= |
2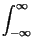 x+ x+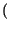 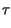 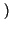 e-j e-j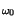 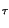 h+ h+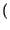 t - t - 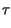 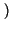 e-j e-j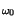 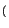 t - t - 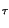 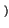 d d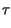 = = |
| |
= |
2e-j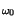 t t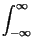 x+ x+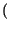 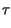 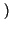 h+ h+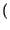 t - t - 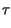 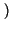 d d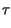 = 2e-j = 2e-j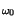 ty+ ty+ t t = = 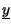  t t |
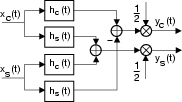
Deriviamo infine le espressioni di
yc t
t ed
ys
ed
ys t
t in funzione delle C.A. di B.F.
di
x
in funzione delle C.A. di B.F.
di
x t
t :
:
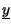
=
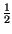
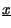
*
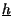
=
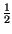
 xc
xc +
jxs![$\displaystyle \left.\vphantom{ x_{c}+jx_{s}}\right]$](img2521.gif)
*
 hc
hc +
jhs![$\displaystyle \left.\vphantom{ h_{c}+jh_{s}}\right]$](img2523.gif)
=
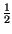
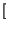 xc
xc*
hc -
xs*
hs![$\displaystyle \left.\vphantom{ x_{c}*h_{c}-x_{s}*h_{s}}\right]$](img2525.gif)
+
j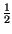
 xs
xs*
hc +
xc*
hs![$\displaystyle \left.\vphantom{ x_{s}*h_{c}+x_{c}*h_{s}}\right]$](img2527.gif)
e dunque:
Intermodulazione tra C.A. di B.F.
Osservando il risultato ottenuto, notiamo come sia
yc t
t che
ys
che
ys t
t dipendano in generale da entrambe
xc
dipendano in generale da entrambe
xc t
t e
xs
e
xs t
t : questo fenomeno prende il nome di intermodulazione
tra componenti analogiche di bassa frequenza, ed è fonte di una distorsione
ineliminabile in banda base. Infatti, le informazioni contenute in
xc
: questo fenomeno prende il nome di intermodulazione
tra componenti analogiche di bassa frequenza, ed è fonte di una distorsione
ineliminabile in banda base. Infatti, le informazioni contenute in
xc t
t ed
xs
ed
xs t
t sono ora mescolate in modo tale che, anche disponendo
sia di
yc
sono ora mescolate in modo tale che, anche disponendo
sia di
yc t
t che di
ys
che di
ys t
t , non
possono essere separate. Gli unici casi in cui ciò non si verifica sono
relativi all'evenienza che
, non
possono essere separate. Gli unici casi in cui ciò non si verifica sono
relativi all'evenienza che
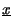
 t
t oppure
oppure
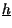
 t
t presentino una sola delle due C.A. di B.F., ossia almeno
uno dei due sia solo reale o solo immaginario.
presentino una sola delle due C.A. di B.F., ossia almeno
uno dei due sia solo reale o solo immaginario.
Ad esempio, se
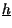
 t
t = hc
= hc t
t , si
ottiene
, si
ottiene
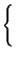
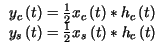 e le componenti trasmesse
xc
e le componenti trasmesse
xc t
t e
xs
e
xs t
t possono essere ri-ottenute a partire da
yc
possono essere ri-ottenute a partire da
yc t
t e
ys
e
ys t
t mediante un procedimento di equalizzazione, che consiste nell'utilizzo
di un filtro
geq
mediante un procedimento di equalizzazione, che consiste nell'utilizzo
di un filtro
geq t
t la cui risposta in frequenza risulta
Geq
la cui risposta in frequenza risulta
Geq f
f = 1/Hc
= 1/Hc f
f , permettendo di ottenere
, permettendo di ottenere
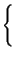
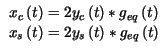 .
.
Sottosezioni





Avanti: Condizioni per t reale
Su: Transito dei segnali in banda traslata
Indietro: Transito dei segnali in banda traslata
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01

![]() t
t![]() = x+
= x+![]() t
t![]() *h+
*h+![]() t
t![]() . Infatti8.19:
. Infatti8.19:
![]() t
t![]() ed
ys
ed
ys![]() t
t![]() in funzione delle C.A. di B.F.
di
x
in funzione delle C.A. di B.F.
di
x![]() t
t![]() :
:
![$\displaystyle \begin{array}{c}
y_{c}\left( t\right) =\frac{1}{2}\left[ x_{c}\le...
...left( t\right) +x_{c}\left( t\right) *h_{s}\left( t\right) \right]
\end{array}$](img2529.gif)
![]()
![]() t
t![]() = hc
= hc![]() t
t![]() , si
ottiene
, si
ottiene
![]()
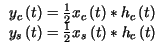 e le componenti trasmesse
xc
e le componenti trasmesse
xc![]() t
t![]() e
xs
e
xs![]() t
t![]() possono essere ri-ottenute a partire da
yc
possono essere ri-ottenute a partire da
yc![]() t
t![]() e
ys
e
ys![]() t
t![]() mediante un procedimento di equalizzazione, che consiste nell'utilizzo
di un filtro
geq
mediante un procedimento di equalizzazione, che consiste nell'utilizzo
di un filtro
geq![]() t
t![]() la cui risposta in frequenza risulta
Geq
la cui risposta in frequenza risulta
Geq![]() f
f![]() = 1/Hc
= 1/Hc![]() f
f![]() , permettendo di ottenere
, permettendo di ottenere
![]()
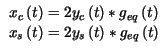 .
.