next up previous contents index
Avanti: Serie Trigonometrica Su: Segnali reali Indietro: Segnali reali   Indice   Indice analitico

Simmetria Coniugata

I coefficienti della serie di Fourier possono essere calcolati anche per segnali complessi; nel caso particolare di x$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$ reale i coefficienti di Fourier risultano godere della proprietà di simmetria coniugata, espressa come

X-n = X*n

e che esprime la circostanza che i coefficienti con indice n negativo possiedono una parte reale uguale a quella dei coefficienti con (uguale) indice positivo, e parte immaginaria cambiata di segno2.4. Ciò comporta una proprietà analoga per il modulo e la fase di $ \left\{\vphantom{ X_{n}}\right.$Xn$ \left.\vphantom{ X_{n}}\right\}$, e dunque possiamo scrivere:

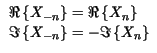x$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$  Reale     $\displaystyle \Leftrightarrow$    $\displaystyle \left\{\vphantom{ \begin{array}{l} \Re \left\{ X_{-n}\right\} =\R... ...\ \Im \left\{ X_{-n}\right\} =-\Im \left\{ X_{n}\right\} \end{array}}\right.$$\displaystyle \begin{array}{l} \Re \left\{ X_{-n}\right\} =\Re \left\{ X_{n}\right\} \\ \Im \left\{ X_{-n}\right\} =-\Im \left\{ X_{n}\right\} \end{array}$ ;  $\displaystyle \left\{\vphantom{ \begin{array}{l} \left\vert X_{-n}\right\vert =... ... 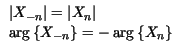\arg \left\{ X_{-n}\right\} =-\arg \left\{ X_{n}\right\} \end{array}}\right.$$\displaystyle \begin{array}{l} \left\vert X_{-n}\right\vert =\left\vert X_{n}\r... ...vert \\ \arg \left\{ X_{-n}\right\} =-\arg \left\{ X_{n}\right\} \end{array}$

0.300000
\resizebox* {0.3\textwidth}{!}{\includegraphics{cap2/f2.1.3.ps}}

Tali relazioni evidenziano come, per x$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$ reale, gli Xn risultano dotati di modulo pari e fase dispari, ovvero parte reale pari e parte immaginaria dispari.

Confrontando la formula di ricostruzione


x$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$ = $ \sum^{\infty }_{n=-\infty }$Xn ej2$\scriptstyle \pi$nFt

con quella


x$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$ = $ {\frac{1}{2}}$$ \left\{\vphantom{ \underline{x}\hbox {e}^{j2\pi f_{0}t}+\underline{x}^{*}\hbox {e}^{-j2\pi f_{0}t}}\right.$$ \underline{x}$ej2$\scriptstyle \pi$f0t + $ \underline{x}^{*}_{}$e-j2$\scriptstyle \pi$f0t$ \left.\vphantom{ \underline{x}\hbox {e}^{j2\pi f_{0}t}+\underline{x}^{*}\hbox {e}^{-j2\pi f_{0}t}}\right\}$


ricavata al § 2.1.3 per il caso di un coseno, e tenendo conto della proprietà di simmetria coniugata X-n = X*n, si nota come un segnale reale possa essere pensato composto a partire da un insieme infinito di fasori (pari alla metà dei coefficienti Xn), rotante ognuno con una velocità angolare $ \omega_{n}^{}$ = 2$ \pi$nF multipla della frequenza fondamentale.

next up previous contents index
Avanti: Serie Trigonometrica Su: Segnali reali Indietro: Segnali reali   Indice   Indice analitico
alef@infocom.uniroma1.it
2001-06-01