Il calcolo della Pe e si basa su quello relativo alle probabilitÓ
di errore Pen condizionato alle singole portanti. Dato che la portante
n-esima trasporta Mn bit/simbolo, la probabilitÓ che un bit
generico provenga dalla portante n-esima risulta pari a
Pr![]() n
n![]() =
= ![]() e quindi la probabilitÓ che sia errato Ŕ pari a
e quindi la probabilitÓ che sia errato Ŕ pari a
La Pen dipende dal numero di livelli
Ln = 2Mn scelto
per la portante n-esima, e dal rapporto
![]()
![]()
![]() locale.
locale.
Per determinare il valore di Pen conviene applicare i risultati
trovati al § 11.3.1 per la modulazione QAM, particolarizzati
al caso attuale, in cui si adottano impulsi rettangolari di durata
T0 = ![]() .
Attribuendo ai punti delle costellazioni gruppi di bit secondo la codifica di
Gray, risulta
.
Attribuendo ai punti delle costellazioni gruppi di bit secondo la codifica di
Gray, risulta
Per il calcolo di
Per quanto riguarda
![]()
![]() , si tratta di applicare
la (11.12) alla sequenza
, si tratta di applicare
la (11.12) alla sequenza
![]()
![]() -1
-1![]()
![]()
![]() hTc
hTc![]()
![]() dei campioni dell'inviluppo complesso del rumore, e determinare il valore
dei campioni dell'inviluppo complesso del rumore, e determinare il valore
Mostriamo ora come, per N sufficientemente elevato, la (11.15)
possa essere calcolata in funzione dei campioni di
Z![]() f
f![]() =
= ![]()
![]() z
z![]() t
t![]()
![]() ,
ed in particolare di come risulti
,
ed in particolare di come risulti
![]()
![]()
![]()
![]() .
. ![]() Z
Z![]() f
f![]()
![]()
![]() 4
4![]() .
. ![]() N
N![]() fn
fn![]() .
.
Analizzando i termini che compaiono in (11.16), osserviamo che il
prodotto
![]()
![]()
![]() t
t![]() ej2
ej2![]()
![]() ha trasformata pari a
ha trasformata pari a
![]()
![]()
![]() f
f![]() , translata
in frequenza di
-
, translata
in frequenza di
- ![]() = -
= - ![]() , ovvero
, ovvero
Dato che
![]()
![]()
![]() f
f![]() Ŕ limitato in banda
tra
Ŕ limitato in banda
tra
![]()
![]() , allora
Z
, allora
Z![]() f
f![]() Ŕ limitato
in una banda compresa tra f = 0 ed f = N
Ŕ limitato
in una banda compresa tra f = 0 ed f = N![]() , e
z
, e
z![]() t
t![]() Ŕ perfettamente rappresentato dai suoi campioni
z
Ŕ perfettamente rappresentato dai suoi campioni
z![]() m
m![]() = z
= z![]() mTc
mTc![]() che compaiono nella (11.15); in particolare, per N sufficientemente
elevato, si ottiene11.25 che
che compaiono nella (11.15); in particolare, per N sufficientemente
elevato, si ottiene11.25 che
| = | 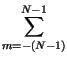 z z |
||
| = | |||
| = | 4 |
in cui si Ŕ tenuto conto che
![]()
![]()
![]() f
f![]() = 4
= 4![]() N+
N+![]() f + f0
f + f0![]() e si Ŕ indicata la densitÓ di potenza in ingresso come
e si Ŕ indicata la densitÓ di potenza in ingresso come
![]() N
N![]() f
f![]() =
= ![]() .
.
Siamo finalmente in grado di scrivere
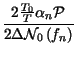 =
=
Se
![]() N
N![]() f
f![]() non dipende da f, possiamo
scrivere
non dipende da f, possiamo
scrivere
Proviamo a verificare se la modulazione OFDM Ŕ vantaggiosa in termini
di prestazioni, per una medesima occupazione di banda ed a paritÓ di potenza.
Nel caso in cui il tempo di guardia
Tg = T - T0 sia nullo, in presenza
di rumore bianco, e scegliendo un intervallo di simbolo
T0 = ![]() da cui derivare
MOFDM = T0 . fb,
Mn =
da cui derivare
MOFDM = T0 . fb,
Mn = ![]() e
e
![]() =
= ![]() , si ottengono valori
, si ottengono valori
![]() uguali per le diverse portanti, a cui corrisponde il miglior valore di
uguali per le diverse portanti, a cui corrisponde il miglior valore di
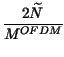
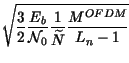
Nel caso in cui si adotti una modulazione a portante singola con impulso a coseno
rialzato e roff-off
![]() =
= ![]() - 1, si determina una
occupazione di banda pari a
B = fL
- 1, si determina una
occupazione di banda pari a
B = fL![]() 1 +
1 + ![]()
![]() che, se eguagliata
a quella del caso OFDM, fornisce
fL =
che, se eguagliata
a quella del caso OFDM, fornisce
fL = ![]()
![]() =
= ![]() e quindi
MQAM =
e quindi
MQAM = ![]() =
= ![]() .
Pertanto in questo caso si ottiene
.
Pertanto in questo caso si ottiene
| PeQAM | = | 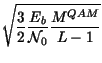 |
|
| = | 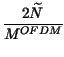 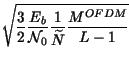 |
E allora dov'Ŕ la convenienza ? E' il tema delle prossime sottosezioni.