next up previous contents index
Avanti: Statistiche dei Processi Su: Correlazione e Covarianza Indietro: Correlazione   Indice   Indice analitico

Covarianza e Indipendenza Statistica

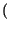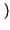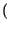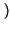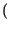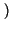Nel caso in cui le due v.a. siano statisticamente indipendenti, e cioè si possa scrivere pX1X2$ \left(\vphantom{ x_{1},x_{2};t_{1},t_{2}}\right.$x1, x2;t1, t2$ \left.\vphantom{ x_{1},x_{2};t_{1},t_{2}}\right)$ = p$ \left(\vphantom{ x_{1}}\right.$x1$ \left.\vphantom{ x_{1}}\right)$p$ \left(\vphantom{ x_{2}}\right.$x2$ \left.\vphantom{ x_{2}}\right)$(7.3), l'integrale che definisce la correlazione si fattorizza e pertanto

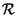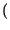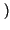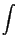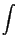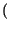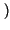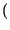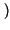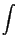$\displaystyle \mathcal {R}$X$\displaystyle \left(\vphantom{ x_{1},x_{2}}\right.$x1, x2$\displaystyle \left.\vphantom{ x_{1},x_{2}}\right)$ = $\displaystyle \int$$\displaystyle \int$x1x2p$\displaystyle \left(\vphantom{ x_{1}}\right.$x1$\displaystyle \left.\vphantom{ x_{1}}\right)$p$\displaystyle \left(\vphantom{ x_{2}}\right.$x2$\displaystyle \left.\vphantom{ x_{2}}\right)$dx1dx2 = $\displaystyle \int$x1p$\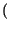displaystyle \left(\vphantom{ x_{1}}\right.$x1$\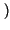displaystyle \left.\vphantom{ x_{1}}\right)$dx1 . 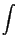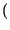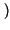$\displaystyle \int$x2p$\displaystyle \left(\vphantom{ x_{2}}\right.$x2$\displaystyle \left.\vphantom{ x_{2}}\right)$dx2 =  
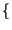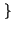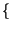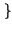  = E$\displaystyle \left\{\vphantom{ x_{1}}\right.$x1$\displaystyle \left.\vphantom{ x_{1}}\right\}$E$\displaystyle \left\{\vphantom{ x_{2}}\right.$x2$\displaystyle \left.\vphantom{ x_{2}}\right\}$ = mX1mX2  

Se a questo punto definiamo covarianza il momento misto centrato

$\displaystyle \sigma$$\displaystyle \left(\vphantom{ x_{1},x_{2}}\right.$x1, x2$\displaystyle \left.\vphantom{ x_{1},x_{2}}\right)$ = E$\displaystyle \left\{\vphantom{ \left( x_{1}-m_{X_{1}}\right) \left( x_{2}-m_{X_{2}}\right) }\right.$$\displaystyle \left(\vphantom{ x_{1}-m_{X_{1}}}\right.$x1 - mX1$\displaystyle \left.\vphantom{ x_{1}-m_{X_{1}}}\right)$$\displaystyle \left(\vphantom{ x_{2}-m_{X_{2}}}\right.$x2 - mX2$\displaystyle \left.\vphantom{ x_{2}-m_{X_{2}}}\right)$ $\displaystyle \left.\vphantom{ \left( x_{1}-m_{X_{1}}\right) \left( x_{2}-m_{X_{2}}\right) }\right\}$ = E$\displaystyle \left\{\vphantom{ x_{1}x_{2}}\right.$x1x2$\displaystyle \left.\vphantom{ x_{1}x_{2}}\right\}$ - mX1mX2 = $\displaystyle \mathcal {R}$X$\displaystyle \left(\vphantom{ x_{1},x_{2}}\right.$x1, x2$\displaystyle \left.\vphantom{ x_{1},x_{2}}\right)$ - mX1mX2

otteniamo7.4 il risultato che

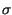
Se due variabili aleatorie x1 ed x2 sono statisticamente indipendenti, queste si dicono INCORRELATE, in quanto la covarianza $ \sigma$$ \left(\vphantom{ x_{1}x_{2}}\right.$x1x2$ \left.\vphantom{ x_{1}x_{2}}\right)$ è nulla7.5.
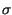
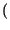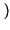La proprietà esposta ha valore in una sola direzione, in quanto se due v.a. esibiscono $ \sigma$$ \left(\vphantom{ x_{1},x_{2}}\right.$x1, x2$ \left.\vphantom{ x_{1},x_{2}}\right)$ = 0 non è detto che siano statisticamente indipendenti7.6. L'unico caso in cui ciò si verifica, è quello relativo alle variabili aleatorie estratte da un processo gaussiano.

next up previous contents index
Avanti: Statistiche dei Processi Su: Correlazione e Covarianza Indietro: Correlazione   Indice   Indice analitico
alef@infocom.uniroma1.it
2001-06-01