Avanti: Correlazione
Su: Densità Spettrale e Filtraggio
Indietro: Densità Spettrale e Filtraggio
Indice
Indice analitico
Abbiamo già osservato come la caratterizzazione statistica del primo ordine
pX x
x di un processo
di un processo
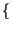 x
x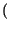 t,
t,
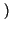
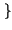 stazionario ergodico, consenta il calcolo di valor medio mx e varianza
stazionario ergodico, consenta il calcolo di valor medio mx e varianza
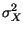 , nonché della potenza
, nonché della potenza
 X = EX
X = EX x2
x2 =
= 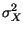 -
- 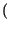 mx
mx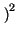 ,
valida per una qualunque realizzazione
,
valida per una qualunque realizzazione  del processo. Definiamo
ora una statistica del secondo ordine che permetterà di determinare anche
lo spettro di densità di potenza delle realizzazioni del processo.
del processo. Definiamo
ora una statistica del secondo ordine che permetterà di determinare anche
lo spettro di densità di potenza delle realizzazioni del processo.
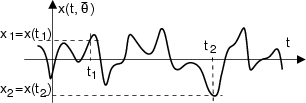
La statistica di secondo ordine si basa sulla considerazione di 2 istanti t1
e t2, in corrispondenza dei quali estraiamo, da una realizzazione
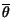 di un processo
x
di un processo
x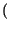 t,
t,
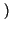 , due
variabili aleatorie
x1 = x
, due
variabili aleatorie
x1 = x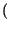 t1
t1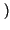 ,
x2 = x
,
x2 = x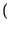 t2
t2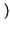 .
Al variare della realizzazione campionata, tutte le coppie di valori estratti
sono altrettante determinazioni di una variabile aleatoria bidimensionale, descritta
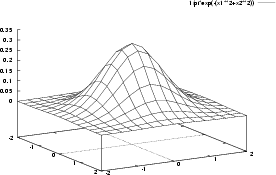
da una densità di probabilità congiunta
pX1X2
.
Al variare della realizzazione campionata, tutte le coppie di valori estratti
sono altrettante determinazioni di una variabile aleatoria bidimensionale, descritta
da una densità di probabilità congiunta
pX1X2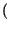 x1x2;t1t2
x1x2;t1t2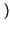 ,
che in linea di principio dipende anche dagli istanti t1 e t2.
,
che in linea di principio dipende anche dagli istanti t1 e t2.
La figura a fianco esemplifica l'operazione di campionamento di una realizzazione,
e mostra come la densità congiunta sottenda un volume unitario, e descriva con
il suo andamento le regioni del piano
x1x2 in cui cadono un maggior
numero di coppie (ovvero dove la probabilità è più densa).
Sottosezioni





Avanti: Correlazione
Su: Densità Spettrale e Filtraggio
Indietro: Densità Spettrale e Filtraggio
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() x
x![]() di un processo
di un processo
![]() x
x![]() t,
t,![]()
![]()
![]() stazionario ergodico, consenta il calcolo di valor medio mx e varianza
stazionario ergodico, consenta il calcolo di valor medio mx e varianza
![]() , nonché della potenza
, nonché della potenza
![]() X = EX
X = EX![]() x2
x2![]() =
= ![]() -
- ![]() mx
mx![]() ,
valida per una qualunque realizzazione
,
valida per una qualunque realizzazione ![]() del processo. Definiamo
ora una statistica del secondo ordine che permetterà di determinare anche
lo spettro di densità di potenza delle realizzazioni del processo.
del processo. Definiamo
ora una statistica del secondo ordine che permetterà di determinare anche
lo spettro di densità di potenza delle realizzazioni del processo.