Avanti: Proprietà dell'autocorrelazione
Su: Correlazione e Covarianza
Indietro: Statistiche dei Processi
Indice
Indice analitico
La media temporale
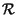 x
x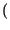

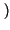 appena introdotta
prende il nome di integrale di autocorrelazione, ed è definito anche
per segnali di energia, come
appena introdotta
prende il nome di integrale di autocorrelazione, ed è definito anche
per segnali di energia, come
in cui l'operatore di coniugato generalizza l'operazione anche al caso di segnali
complessi. Simile, ma diversa, è la definizione di integrale di intercorrelazione,
che esprime lo stesso calcolo, ma relativo a variabili aleatorie estratte da
due processi diversi:
L'integrale di autocorrelazione è anche detto funzione di autocorrelazione,
in quanto il suo argomento è un tempo (l'intervallo tra due campioni) e dunque
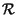 x
x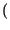

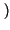 può essere visto come un segnale
(funzione di t =
può essere visto come un segnale
(funzione di t =  ). Nello studio abbiamo già incontrato un integrale
(di convoluzione) il cui risultato è una funzione del tempo; la somiglianza
tra i due è più profonda di una semplice analogia, in quanto si può scrivere
in cui * è il consueto simbolo di convoluzione7.8.
). Nello studio abbiamo già incontrato un integrale
(di convoluzione) il cui risultato è una funzione del tempo; la somiglianza
tra i due è più profonda di una semplice analogia, in quanto si può scrivere
in cui * è il consueto simbolo di convoluzione7.8.
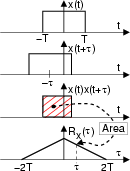
In base a quest'ultima osservazione otteniamo che la costruzione grafica, che
fornisce il risultato dell'integrale di autocorrelazione, è del tutto simile
a quella già illustrata per la convoluzione, con la differenza che ora non si
effettuano ribaltamenti di asse. La figura a lato ne illustra l'applicazione
ad un caso noto, per il quale
x t
t = x*
= x*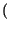 - t
- t ,
e che fornisce quindi lo stesso risultato di
x
,
e che fornisce quindi lo stesso risultato di
x t
t *x
*x t
t .
.
Sottosezioni





Avanti: Proprietà dell'autocorrelazione
Su: Correlazione e Covarianza
Indietro: Statistiche dei Processi
Indice
Indice analitico
alef@infocom.uniroma1.it
2001-06-01
![]() x
x![]()
![]()
![]() appena introdotta
prende il nome di integrale di autocorrelazione, ed è definito anche
per segnali di energia, come
appena introdotta
prende il nome di integrale di autocorrelazione, ed è definito anche
per segnali di energia, come