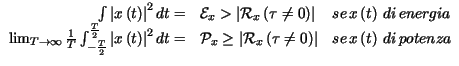Elenchiamo ora alcune caratteristiche della funzione di autocorrelazione:
Se consideriamo i segnali
x![]() t
t![]() e
y
e
y![]() t
t![]() = x
= x![]() t +
t + ![]()
![]() ,
le rispettive autocorrelazioni
,
le rispettive autocorrelazioni
![]() x
x![]()
![]()
![]() ed
ed
![]() y
y![]()
![]()
![]() sono identiche7.9. Questo risultato mostra come l'autocorrelazione non tenga conto dell'informazione
legata alla fase dei segnali: infatti
x
sono identiche7.9. Questo risultato mostra come l'autocorrelazione non tenga conto dell'informazione
legata alla fase dei segnali: infatti
x![]() t
t![]() e
y
e
y![]() t
t![]() hanno la stessa densitÓ spettrale, a meno di un contributo di fase lineare,
ed hanno uguale autocorrelazione.
hanno la stessa densitÓ spettrale, a meno di un contributo di fase lineare,
ed hanno uguale autocorrelazione.
La funzione di autocorrelazione di un segnale di durata limitata Ŕ anch'essa a durata limitata, e di estensione doppia rispetto alla durata del segnale originario.
L'autocorrelazione di un segnale periodico di periodo T Ŕ anch'essa periodica,
con lo stesso periodo. Infatti per ![]() = nT il secondo fattore integrando
Ŕ traslato di un numero intero di periodi.
= nT il secondo fattore integrando
Ŕ traslato di un numero intero di periodi.
Illustriamo ora invece due proprietÓ fondamentali:
La
![]() x
x![]()
![]()
![]() calcolata in
calcolata in ![]() = 0 fornisce
il valore massimo di
= 0 fornisce
il valore massimo di
![]() x
x![]()
![]()
![]() per qualunque
altro valore di
per qualunque
altro valore di ![]() . In particolare,
. In particolare,
![]() x
x![]()
![]() = 0
= 0![]() Ŕ uguale alla potenza del segnale
x
Ŕ uguale alla potenza del segnale
x![]() t
t![]() , od all'energia se
x
, od all'energia se
x![]() t
t![]() Ŕ di energia.
Ŕ di energia.