Segnale modulante sinusoidale

Ponendo m$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = cos(2$\pi$wt), si ottiene che la fase modulata $\alpha$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ e la frequenza istantanea f_i$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ per i due casi PM ed FM, relativi al segnale x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = acos(2$\pi$f₀t + $\alpha$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$), risultano:

	$\alpha$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$		fi$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$		$\Delta$$\alpha$	$\Delta$f
PM	k$\phi$cos$\left(\vphantom{ 2\pi wt}\right.$2$\pi$wt$\left.\vphantom{ 2\pi wt}\right)$		f0 + wk$\phi$sin$\left(\vphantom{ 2\pi wt}\right.$2$\pi$wt$\left.\vphantom{ 2\pi wt}\right)$		k$\phi$	wk$\phi$
FM	2$\pi$kf$\int_{-\infty }^{t}$m($\tau$)d$\tau$ = ${\frac{k_{f}}{w}}$sin$\left(\vphantom{ 2\pi wt}\right.$2$\pi$wt$\left.\vphantom{ 2\pi wt}\right)$		f0 + kfcos$\left(\vphantom{ 2\pi wt}\right.$2$\pi$wt$\left.\vphantom{ 2\pi wt}\right)$		${\frac{k_{f}}{w}}$	kf

<><>

in cui si è anche indicata la massima deviazione di fase $\Delta$$\alpha$ = max$\left\{\vphantom{ \left\vert \alpha \left( t\right) \right\vert }\right.$$\left\vert\vphantom{ \alpha \left( t\right) }\right.$$\alpha$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ \alpha \left( t\right) }\right\vert$ $\left.\vphantom{ \left\vert \alpha \left( t\right) \right\vert }\right\}$ e di frequenza $\Delta$f = max$\left\{\vphantom{ \left\vert f_{i}\left( t\right) -f_{0}\right\vert }\right.$$\left\vert\vphantom{ f_{i}\left( t\right) -f_{0}}\right.$f_i$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ - f₀$\left.\vphantom{ f_{i}\left( t\right) -f_{0}}\right\vert$ $\left.\vphantom{ \left\vert f_{i}\left( t\right) -f_{0}\right\vert }\right\}$. Notiamo subito che, in entrambi i casi, sia la fase $\alpha$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ che la frequenza istantanea f_i$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ variano sinusoidalmente con periodo ${\frac{1}{w}}$; nel caso PM l'entità di $\Delta$f aumenta con w, mentre nell'FM la $\Delta$$\alpha$ diminuisce con w. Nel seguito si farà riferimento all'indice di modulazione angolare $\beta$, corrispondente alla massima escursione della fase $\Delta$$\alpha$, che risulta:

$$\beta$$ = $$\left\{\vphantom{ \begin{array}{cc} k_{\phi } & \hbox {(PM)}\\ \frac{k_{f}}{w} & \hbox {(FM)} \end{array}}\right.$$$$\begin{array}{cc} k_{\phi } & \hbox {(PM)}\\ \frac{k_{f}}{w} & \hbox {(FM)} \end{array}$$

Con questa convenzione, possiamo trattare congiuntamente entrambi i casi PM ed FM riscrivendo l'inviluppo complesso come ^9.23

$$\underline{x}$$$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = ae^{j$\beta$sin(2$\pi$wt)}

Notiamo ora che $\underline{x}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ è periodico di periodo ${\frac{1}{w}}$, e dunque per esso vale lo sviluppo in serie di Fourier $\underline{x}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = a$\sum_{n=-\infty }^{\infty }$X_ne^j2$\pi$nwt, i cui coefficienti risultano

X_n = w$$\int_{-\frac{1}{2w}}^{\frac{1}{2w}}$$e^{j$\beta$sin(2$\pi$wt)}e^-j2$\pi$nwtdt = $$\mathcal {J}$$_n$$\left(\vphantom{ \beta }\right.$$$$\beta$$ $$\left.\vphantom{ \beta }\right)$$

ovvero sono pari alle funzioni di Bessel del primo tipo, ordine n ed argomento $\beta$. Queste hanno l'andamento mostrato in figura, assieme alle proprietà che le caratterizzano:

 

 

• $\mathcal {J}$_n$\left(\vphantom{ \beta }\right.$$\beta$ $\left.\vphantom{ \beta }\right)$ è reale con $\forall$n,$\beta$
• $\left\{\vphantom{ \begin{array}{rcll} \mathcal{J}_{n}\left( \beta \right) & = ... ...-\mathcal{J}_{-n}\left( \beta \right) & n\, \hbox {dispari} \end{array}}\right.$$\begin{array}{rcll} \mathcal{J}_{n}\left( \beta \right) & = & \mathcal{J}_{-n}... ...) & = & -\mathcal{J}_{-n}\left( \beta \right) & n\, \hbox {dispari} \end{array}$
• $\sum_{n=-\infty }^{+\infty }$$\mathcal {J}$_n²$\left(\vphantom{ \beta }\right.$$\beta$ $\left.\vphantom{ \beta }\right)$ = 1
• $\mathcal {J}$_n$\left(\vphantom{ \beta }\right.$$\beta$ $\left.\vphantom{ \beta }\right)$ $\simeq$ 0 con n > $\beta$ se $\beta$ $\gg$ 1

 

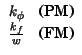
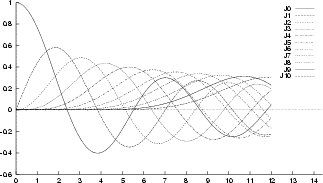
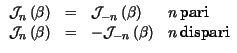
e quindi i valori di X_n si ottengono tracciando una linea verticale nel diagramma di figura in corrispondenza del valore $\beta$ adottato, e individuando il valore di ciascuna $\mathcal {J}$_n per quel $\beta$. Osserviamo ora che l'ultima proprietà mostra come, in presenza di un valore di $\beta$ elevato, le funzioni di Bessel di ordine n > $\beta$ siano praticamente nulle: è quindi lecito in tal caso limitare lo sviluppo in serie di Fourier di $\underline{x}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ ai primi $\beta$ termini (positivi e negativi), ovvero: $\underline{x}_{FM}^{}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\simeq$ a$\sum_{n=-\beta }^{\beta }$$\mathcal {J}$_n$\left(\vphantom{ \beta }\right.$$\beta$ $\left.\vphantom{ \beta }\right)$e^j2$\pi$nwt. Pertanto, il segnale modulato x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\Re$$\left\{\vphantom{ \underline{x}(t)\hbox {e}^{j\omega _{0}t}}\right.$$\underline{x}$(t)e^{j$\omega_{0}$t}$\left.\vphantom{ \underline{x}(t)\hbox {e}^{j\omega _{0}t}}\right\}$ risulta:

x$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ $$\simeq$$ a$$\sum_{n=-\beta }^{\beta }$$$$\mathcal {J}$$_n$$\left(\vphantom{ \beta }\right.$$$$\beta$$ $$\left.\vphantom{ \beta }\right)$$cos 2$$\pi$$(f₀ + nw)t

e quindi lo spettro di densità di potenza $\mathcal {P}$_x$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = ${\frac{1}{4}}$$\left[\vphantom{ \mathcal{P}_{\underline{x}}\left( f-f_{0}\right) +\mathcal{P}_{\underline{x}}\left( f+f_{0}\right) }\right.$$\mathcal {P}$_{$\underline{x}$}$\left(\vphantom{ f-f_{0}}\right.$f - f₀$\left.\vphantom{ f-f_{0}}\right)$ + $\mathcal {P}$_{$\underline{x}$}$\left(\vphantom{ f+f_{0}}\right.$f + f₀$\left.\vphantom{ f+f_{0}}\right)$ $\left.\vphantom{ \mathcal{P}_{\underline{x}}\left( f-f_{0}\right) +\mathcal{P}_{\underline{x}}\left( f+f_{0}\right) }\right]$ ha espressione

$$\mathcal {P}$$_x$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ $$\simeq$$ $${\frac{a^{2}}{4}}$$$$\sum_{n=-\beta }^{\beta }$$$$\left\vert\vphantom{ \mathcal{J}_{n}\left( \beta \right) }\right.$$$$\mathcal {J}$$_n$$\left(\vphantom{ \beta }\right.$$$$\beta$$ $$\left.\vphantom{ \beta }\right)$$ $$\left.\vphantom{ \mathcal{J}_{n}\left( \beta \right) }\right\vert^{2}_{}$$$$\left[\vphantom{ \delta \left( f-f_{0}+nw\right) +\delta \left( f+f_{0}+nw\right) }\right.$$$$\delta$$$$\left(\vphantom{ f-f_{0}+nw}\right.$$f - f₀ + nw$$\left.\vphantom{ f-f_{0}+nw}\right)$$ + $$\delta$$$$\left(\vphantom{ f+f_{0}+nw}\right.$$f + f₀ + nw$$\left.\vphantom{ f+f_{0}+nw}\right)$$ $$\left.\vphantom{ \delta \left( f-f_{0}+nw\right) +\delta \left( f+f_{0}+nw\right) }\right]$$

ed è formato da impulsi centrati a frequenze f = $\pm$f₀$\pm$nw (^9.24).

La fig. 9.1 mette a confronto $\left\vert\vphantom{ X\left( f\right) }\right.$X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ X\left( f\right) }\right\vert$ per f vicino ad f₀, ovvero mostra $\left\vert\vphantom{ X^{+}\left( f\right) }\right.$X⁺$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ X^{+}\left( f\right) }\right\vert$ = ${\frac{a}{2}}$$\sum_{n=-\beta }^{\beta }$$\left\vert\vphantom{ \mathcal{J}_{n}\left( \beta \right) }\right.$$\mathcal {J}$_n$\left(\vphantom{ \beta }\right.$$\beta$ $\left.\vphantom{ \beta }\right)$ $\left.\vphantom{ \mathcal{J}_{n}\left( \beta \right) }\right\vert$$\delta$$\left(\vphantom{ f-f_{0}+nw}\right.$f - f₀ + nw$\left.\vphantom{ f-f_{0}+nw}\right)$, calcolato per diversi valori di $\beta$, mantenendo fisso w oppure K_F (a sinistra e destra rispettivamente), e ci aiuta a comprendere i ragionamenti che seguono.

Figura: di ampiezza per segnale FM a modulazione sinusoidale

Modulazione a basso indice

In questo caso $\beta$ < 1, e tale da rendere trascurabili le funzioni di Bessel $\mathcal {J}$_n$\left(\vphantom{ \beta }\right.$$\beta$ $\left.\vphantom{ \beta }\right)$ con n > 1. Allora, x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ occupa una banda pari a 2w, in modo del tutto simile all'AM-BLD.

Modulazione ad alto indice

In tal caso sono presenti piú funzioni di Bessel, ed il comportamento non lineare tende a legare $\mathcal {P}$_x$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ ai valori assunti da f_i$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = k_fm$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, realizzando una conversione ampiezza $\rightarrow$ frequenza.

In Fig. 9.1 sono evidenziati gli effetti dell'aumento di $\beta$ = ${\frac{k_{f}}{w}}$ nelle due circostanze:

1. Si mantiene w fisso, aumentando k_f. Il numero di righe spettrali a frequenza f₀$\pm$nw aumenta, occupando una banda crescente, e per $\beta$ $\rightarrow$ $\infty$ si verifica che $\mathcal {J}$_n$\left(\vphantom{ \beta }\right.$$\beta$ $\left.\vphantom{ \beta }\right)$ = 0 per n > $\beta$. Pertanto, la banda occupata tende a B = 2$\beta$w = 2${\frac{k_{f}}{w}}$ ^. w = 2k_f;
2. Si mantiene k_f fisso, diminuendo w. La banda occupata tende a ridursi, mentre le nuove righe spettrali a frequenza f₀$\pm$nw si infittiscono. Per $\beta$ $\rightarrow$ $\infty$, la spaziatura w tra le righe spettrali tende ad annullarsi, producendo una $\mathcal {P}$_x$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ praticamente continua, e con una banda B = 2k_f, ossia pari alla massima deviazione di frequenza istantanea $\Delta$f.

Regola di Carson

Come mostrato, nei due casi a basso ed alto indice, la banda occupata da x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ varia tra 2w e 2k_f rispettivamente. Nei casi intermedi, è pratica comune ricorrere all'espressione

B_C $$\simeq$$ 2$$\left(\vphantom{ k_{f}+w}\right.$$k_f + w$$\left.\vphantom{ k_{f}+w}\right)$$ = 2w$$\left(\vphantom{ \beta +1}\right.$$$$\beta$$ + 1$$\left.\vphantom{ \beta +1}\right)$$

nota come Regola di Carson^9.25, che tiene conto di entrambi i fattori che concorrono alla determinazione della banda, e che fornisce i valori esatti sia per $\beta$ $\ll$ 1, che per $\beta$ $\rightarrow$ $\infty$, in entrambi i casi k_f $\rightarrow$ $\infty$ o w $\rightarrow$ 0.

Sebbene la determinazione approssimata della banda mediante la Regola di Carson sia stata ottenuta nel caso di m$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = cos(2$\pi$wt), la stessa espressione è spesso adottata come una buona approssimazione anche per segnali non sinusoidali, ma limitati in banda tra - W e W, e contraddistinti da una $\Delta$f = k_f ^. max$\left\{\vphantom{ \left\vert m\left( t\right) \right\vert }\right.$$\left\vert\vphantom{ m\left( t\right) }\right.$m$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ $\left.\vphantom{ m\left( t\right) }\right\vert$ $\left.\vphantom{ \left\vert m\left( t\right) \right\vert }\right\}$. In tal caso, la regola di Carson si applica ponendo ora B_C $\simeq$ = 2W$\left(\vphantom{ \beta +1}\right.$$\beta$ + 1$\left.\vphantom{ \beta +1}\right)$ con $\beta$ = ${\frac{\Delta f}{W}}$. Per un approfondimento della questione, si veda l'appendice 9.4.6 e la sottosezione 9.3.3.1.

A prima vista, l'estensione del risultato per m$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = cos(2$\pi$wt) al caso qualunque appare piú che ragionevole; il comportamento non lineare della modulazione angolare impedisce però una sua verifica analitica. D'altra parte, i risultati sperimentali mostrano che l'approssimazione fornita dalla banda di Carson può effettivamente costituire una stima plausibile della banda occupata per segnali modulanti qualsiasi.

In base alla regola di Carson, notiamo ora che la banda occupata dal segnale modulato può risultare $\beta$ + 1 volte piú estesa di quella ottenibile mediante modulazione AM. Nonostante questo aumento di banda possa apparire un fatto negativo, vedremo nel capitolo 10 che ciò consente un migliore SNR dopo la demodulazione rispetto al caso AM. Al contrario, se $\beta$ $\ll$ 1, il comportamento si avvicina molto a quello lineare (vedi appendice 9.4.5).