Propagazione luminosa

Dispersione modale

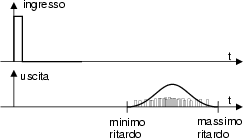
Questo fenomeno è dovuto al fatto che i modi propagazione relativi agli angoli di incidenza più elevati, percorrono di fatto più strada, e dunque impiegano più tempo per giungere a destinazione.

0.400000

Pertanto, ogni singolo impulso luminoso presente in ingresso produce in uscita più impulsi distanziati nel tempo, uno per ogni modo di propagazione. Dato che inoltre avviene un continuo scambio di energia tra i diversi modi, si ottiene che l'uscita sarà un segnale con una sagomatura allargata (vedi figura). L'entità della dispersione temporale (differenza tra ritardo max e min) sarà tanto maggiore quanto più il collegamento è lungo, e quanti più modi partecipano alla propagazione. L'effetto più appariscente del fenomeno descritto consiste nella limitazione della massima frequenza con cui gli impulsi luminosi possono essere posti in ingresso alla fibra; impulsi troppo vicini risulterebbero infatti indistinguibili in uscita. Pertanto la massima frequenza di segnalazione in una fibra ottica ... dipende dalla lunghezza della fibra stessa!

Si chiamano fibre multimodo le fibre ottiche in cui sono presenti più modi di propagazione. Queste sono del tipo STEP INDEX se n cambia in modo brusco, o GRADED INDEX se il core ha un indice graduato. Nel secondo caso la dispersione temporale è ridotta; infatti quando i modi secondari attraversano la sezione periferica del core, incontrano un indice di rifrazione n ridotto, e quindi viaggiano più veloci.

Una diversa (e drastica) soluzione al problema della dispersione temporale, è fornita dalle fibre ottiche monomodo: queste sono realizzate con un core di diametro così piccolo, da permettere la propagazione del solo modo primario.

Ovviamente le ultime due soluzioni (graded index e fibra monomodo) si sono rese possibili grazie ai progressi nei processi di fabbricazione. Per concretizzare il discorso, è sufficiente citare che il diametro del core passa dai 50 $\mu$m per le fibre multimodo, a circa 8 $\mu$m nel caso monomodo.

Attenuazione

 

0.400000

In modo simile ai cavi elettrici, anche le fibre ottiche sono mezzi dissipativi, in quanto parte dell'energia in transito viene assorbita dalla fibra stessa e trasformata in calore. I fenomeni di assorbimento sono legati alla presenza di impurità chimiche, che possono ridurre la trasparenza oppure avere dimensioni (a livello molecolare) comparabili con le lunghezze d'onda in gioco.

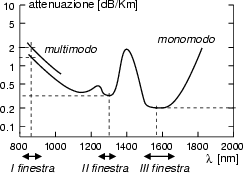
Per questi motivi, la caratteristica di attenuazione chilometrica ha un andamento fortemente dipendente da $\lambda$, e sono stati individuati 3 intervalli di lunghezze d'onda (detti finestre) per i quali l'assorbimento è ridotto, ed in cui sono effettuate le trasmissioni ottiche.

Finestra	I	II	III
$\lambda$	.8÷.9 $\mu$m	1.2÷1.3 $\mu$m	1.5÷1.7 $\mu$m
Ad (dB/Km)	12 (monom.)	.35	.2
	20 (multim.)

<><>

La prima finestra (con attenuazione maggiore) è stata l'unica disponibile agli inizi, a causa dell'assenza di trasduttori affidabili a frequenze inferiori, ed è tuttora usata per collegamenti economici e scarsamente critici. La seconda finestra ha iniziato ad essere usata assieme alle fibre monomodo, grazie all'evoluzione tecnologica dei trasduttori, mentre l'uso della III finestra si è reso possibile dopo essere riusciti a limitare la dispersione cromatica delle fibre (vedi appresso).

Un'altra fonte di attenuazione può avere origine dalle giunzioni tra tratte di fibre ottiche: l'uso di connettori produce una perdita di 0.4 ÷ 1 dB, ed i giunti meccanici $\simeq$ 0.2 dB oppure anche 0,05 dB se ottimizzati per via strumentale. Si possono infine fondere tra loro le fibre, con perdite tra 0,01 e 0,1 dB.

Dispersione cromatica e trasduttori elettro-ottici

Dopo aver ridotto od eliminato il fenomeno di dispersione modale, si è individuata una ulteriore causa di dispersione temporale dell'energia immessa nella fibra ottica: il problema si verifica se il segnale di ingresso non è perfettamente monocromatico, ovvero sono presenti diverse lunghezze d'onda. Dato che il valore dell'indice di rifrazione dipende dalla lunghezza d'onda, $\lambda$ diverse si propagano con velocità differenti e raggiungono l'altro estremo della fibra in tempi sucessivi. La dispersione cromatica della fibra si misura in [psec/Km ^. nm], e dà luogo ad una dispersione temporale tanto maggiore quanto più è lunga la fibra, e quanto più è estesa la gamma cromatica $\Delta$$\lambda$ della sorgente^13.17. Per ridurre il fenomeno è possibile:

• Utilizzare una lunghezza d'onda $\lambda$ per la quale la dispersione cromatica è ridotta. Ad esempio, una fibra di silicio produce una dispersione cromatica 15 volte inferiore a 1.3 $\mu$m che non a 1.5 $\mu$m.
• Scegliere una sorgente con la minima estensione cromatica $\Delta$$\lambda$ possibile.

Per ciò che riguarda il secondo punto, i trasduttori usati per primi sono stati gli economici LED (Light Emitting Diode), che richiedono una circuiteria di interfaccia semplice, sono poco sensibili alle condizioni ambientali, e quindi risultano affidabili. D'altra parte, i LED emettono luce su più lunghezze d'onda, mentre per limitare la dispersione cromatica (e quindi raggiungere frequenze di segnalazione più elevate) occorre ricorrere ai Diodi Laser (LD).

Sorgente	$\lambda$ (nm)	WdT (dBm)	$\Delta$$\lambda$ (nm)
Si LED	850	-16	50
Ge LED	1300	-19	70
InGaAsP LED	1300	-10	120
DFB LASER	1300	-5	1
DFB LASER	1550	-5	0.4
IL/DFB LASER	1550	+2	0.8

<><>

I LASER forniscono anche una maggiore potenza, e quindi divengono indispensabili per coprire distanze maggiori^13.18. D'altra parte sono più costosi, hanno vita media ridotta rispetto ai LED, e richiedono condizioni di lavoro più controllate. Notiamo inoltre che una fibra ottica posta inizialmente in opera mediante sorgenti LED, può essere potenziata (in termini di banda) sostituendo il LED con il LASER.

L'uso di sorgenti che operano in III finestra, che (presentando una attenuazione ridotta) permette di operare con tratte più lunghe, obbliga in generale a ridurre la frequenza di segnalazione, a causa della maggiore dispersione cromatica. Quest'ultima limitazione è stata rimossa da un particolare tipo di fibra, detta dispersion shifted, che presenta un minimo di dispersione cromatica D in III finestra anziché in II, e che raggiunge valori migliori di 3.5 psec/Km ^. nm.

Prodotto Banda-Lunghezza e Codici di linea

Come anticipato, la dispersione cromatica D risulta proporzionale alla lunghezza del collegamento L ed all'estensione cromatica $\Delta$$\lambda$ della sorgente. Se pensiamo di effettuare una trasmissione con codici NRZ e periodo T = ${\frac{1}{f_{L}}}$, ed imponiamo che la dispersione temporale sia non maggiore di ${\frac{1}{4}}$T_L, otteniamo D ^. L ^. $\Delta$$\lambda$ $\leq$ 0.25 ^. T, in cui D è la dispersione cromatica [psec/Km-nm], L è la lunghezza [Km], $\Delta$$\lambda$ è l'estensione cromatica della sorgente [nm], e T è la durata di un bit [psec]. Associando ora il concetto di banda B alla frequenza di segnalazione f_L = ${\frac{1}{T_{L}}}$, si può affermare che il prodotto della banda per la lunghezza è pari al valore

PBL_NRZ = B ^. L = $${\frac{.25}{D\cdot \Delta \lambda }}$$    [Gbps ^. Km]

che è una grandezza dipendente dalla coppia fibra-sorgente^13.19. Inserendo i valori di $\Delta$$\lambda$ (della sorgente) e D (della fibra), si ottiene una costante da usare per calcolare la banda (frequenza) massima trasmissibile per una data lunghezza (o viceversa).

 

0.300000

 

Qualora si usi un codice RZ, i cui simboli hanno durata metà del periodo di bit T, la dispersione temporale tollerabile può essere elevata al 50% di T, e quindi in questo caso il prodotto banda-lunghezza risulta doppio rispetto al caso precedente:

PBL_RZ = $${\frac{.5}{D\cdot \Delta \lambda }}$$ = 2 ^. PBL_NRZ

La tabella seguente riporta i valori di PBL_NRZ per alcune coppie fibra-sorgente.

Fibra	Sorgente	$\lambda$ [nm]	PBL [Gbps . Km]
Multimodo	LED	820	0.013
Graded Index	LED	820	2
Monomodo	LASER	1300	250
Monomodo	LASER	1550	36.8
Monomodo DS	LASER	1550	179

<><>

Esercizio

determinare la lunghezza massima di un collegamento in fibra ottica monomodo, operante con $\lambda$=1.3 $\mu$m, e che garantisca una velocità f_L=417 Mbps, assumendo un guadagno di sistema di 42 dB (ovvero disponendo di una potenza di trasmissione 42 dB maggiore della minima potenza necessaria in ricezione).

Soluzione

Si trova che per $\lambda$=1300 nm, l'attenuazione chilometrica è di 0,35 dB/Km, e questo valore determina una lunghezza non superiore a ${\frac{42}{0.35}}$=120 Km, che identifica il Limite di Attenuazione del collegamento. Verifichiamo quindi che non intervenga un limite più stringente per causa della dispersione cromatica. Supponendo di utilizzare la sorgente laser in grado di conseguire un PBL di 250 Gbps ^. Km, si ottiene una lunghezza massima pari a ${\frac{250.000}{417}}$=600 Km, che costituisce il Limite di Dispersione.

L'esercizio svolto ha lo scopo di mostrare la metodologia di progetto per un collegamento in fibra ottica, in cui vengono calcolati entrambi i limiti di Attenuazione e di Dispersione, e la massima lunghezza del collegamento è determinata dal vincolo più stringente. Nel caso dell'esercizio, la lunghezza è determinata dal limite di attenuazione, ed il progetto può essere rivisto utilizzando una sorgente meno pura per risparmiare, oppure una sorgente più potente per aumentare il guadagno di sistema e conseguentemente migliorare il limite di attenuazione. In questo secondo caso, può essere opportuno prestare attenzione al fatto che, aumentando la potenza di emissione, la purezza cromatica della sorgente può degradare (in quanto si verifica un aumento di $\Delta$$\lambda$ dovuto a fenomeni non lineari) con un conseguente peggioramento del limite di dispersione; è pertanto possibile ricercare la soluzione di migliore compromesso tra potenza di emissione e purezza spettrale.

Qualora non si riesca a rientrare nelle specifiche di progetto con una unica tratta, occorrerà suddividere il collegamento in più tratte, collegate da ripetitori rigenerativi.

Trasduttori elettro-ottici

La conversione del segnale uscente dalla fibra ottica meriterebbe una ampia trattazione approfondita, ma qui ci limitiamo a riferire esclusivamente poche cose fondamentali.

Il trasduttore utilizzato fin dall'inizio, economico ed affidabile, è il diodo P-I-N, che però non è adatto all'impiego con $\lambda$ più elevate. Un secondo tipo di trasduttore molto usato è il diodo APD (Avalanche Photo Detector), caratterizzato da un ``effetto valanga'' che lo rende più sensibile di 10-15 dB rispetto ai P-I-N; d'altra parte però gli APD sono più delicati, e più sensibili alla temperatura.

La tabella che segue riporta i valori di sensibilità W_R (ossia la minima potenza che è necessario ricevere) di diversi fotorivelatori, per una probabilità di errore per bit P_e = 10^-11.

Fotorivelatore	$\lambda$ [nm]	Sensibilità [dBm]	fb [Mbps]
Si P-I-N	850	-48	50
Si APD	850	-58	50
InGaAs P-I-N	1310	-35	420
InGaAs APD	1310	-43	420
InGaAs APD	1550	-37.5	678

<><>

Nella tabella è riportato anche il valore della frequenza di segnalazione f_b a cui si riferisce la sensibilità, in quanto le prestazioni conseguite dal decisore che si trova a valle del trasduttore dipendono, come noto, da ${\frac{E_{b}}{N_{0}}}$, in cui E_b è l'energia per bit che vale E_b = W_R ^. T_b = ${\frac{W_{R}}{f_{b}}}$. Pertanto, i trasduttori dimezzano la sensibilità (che aumenta di 3 dB) se la velocità f_b raddoppia, in quanto si dimezza l'energia per bit E_b. La sensibilità a frequenze diverse da quelle in tabella può quindi essere calcolata come^13.20

W_R$$\left(\vphantom{ f_{b}^{'}}\right.$$f_b^'$$\left.\vphantom{ f_{b}^{'}}\right)$$  [dBm] = W_R$$\left(\vphantom{ f_{b}}\right.$$f_b$$\left.\vphantom{ f_{b}}\right)$$  [dBm] + 10log$${\frac{f_{b}^{'}}{f_{b}}}$$