Proprietà di setacciamento

0.380000  

 

 

 

Osserviamo innanzitutto che il prodotto di un segnale per un impulso unitario dà come risultato lo stesso impulso, con area pari al valore del segnale nell'istante in cui è centrato l'impulso:

x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$$\delta$$\left(\vphantom{ t-\tau }\right.$t - $\tau$ $\left.\vphantom{ t-\tau }\right)$ = x$\left(\vphantom{ \tau }\right.$$\tau$ $\left.\vphantom{ \tau }\right)$$\delta$$\left(\vphantom{ t-\tau }\right.$t - $\tau$ $\left.\vphantom{ t-\tau }\right)$.

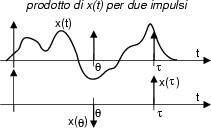
Questa considerazione consente di scrivere il valore di x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ per un istante t = $\tau$, nella forma

x$$\left(\vphantom{ \tau }\right.$$$$\tau$$ $$\left.\vphantom{ \tau }\right)$$ = $$\int^{\infty }_{-\infty }$$x$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$$$\delta$$$$\left(\vphantom{ t-\tau }\right.$$t - $$\tau$$ $$\left.\vphantom{ t-\tau }\right)$$dt

Quest'ultima proprietà è detta di setacciamento (SIEVING in inglese) perché in qualche modo simile all'azione di un setaccio con cui passare la farina, passata la quale... la farina non c'è più, ed al suo posto resta un unico sassolino, come l'unico punto di segnale che è stato campionato dall'impulso e dall'integrale.