




Avanti: Trasformata di una costante
Su: Trasformata di Fourier
Indietro: Prime proprietÓ della trasformata di Fourier
Indice
Indice analitico
E' definito come un segnale
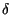 (t)3.6 che vale zero ovunque, tranne per t = 0 dove vale
(t)3.6 che vale zero ovunque, tranne per t = 0 dove vale 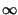 ; per
contro, l'area di
; per
contro, l'area di
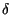 (t) Ŕ unitaria:
(t) Ŕ unitaria:
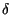
 f
f non Ŕ una funzione in senso matematico, ma il
limite a cui tende una distribuzione. E' prassi rappresentare graficamente
A .
non Ŕ una funzione in senso matematico, ma il
limite a cui tende una distribuzione. E' prassi rappresentare graficamente
A . 
 f
f come una freccia (vedi figura) con scritto accanto il valore dell'area A.
come una freccia (vedi figura) con scritto accanto il valore dell'area A.
Sottosezioni
alef@infocom.uniroma1.it
2001-06-01
![]() (t)3.6 che vale zero ovunque, tranne per t = 0 dove vale
(t)3.6 che vale zero ovunque, tranne per t = 0 dove vale ![]() ; per
contro, l'area di
; per
contro, l'area di
![]() (t) Ŕ unitaria:
(t) Ŕ unitaria:
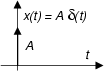
 e
e