Trasformata per segnali periodici

Consideriamo un segnale periodico x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, del quale conosciamo lo sviluppo in serie

x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = $\sum^{\infty }_{n=-\infty }$X_n e^j2$\pi$nFt

Applicando la proprietà di linearità, il risultato per la trasformata di una costante, e ricordando la proprietà della traslazione in frequenza, troviamo^3.8 che la $\mathcal {F}$-trasformata di x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ vale:

X$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\sum^{\infty }_{n=-\infty }$X_n $\delta$$\left(\vphantom{ f-nF}\right.$f - nF$\left.\vphantom{ f-nF}\right)$

Lo spettro di ampiezza di un segnale periodico è quindi costituito da impulsi matematici, situati in corrispondenza delle frequenze armoniche, e di area pari ai rispettivi coefficienti della serie di Fourier.

Un modo alternativo di calcolare la trasformata di segnali periodici è illustrato alla sezione 3.8.

Trasformata di un coseno

Applichiamo il risultato trovato nel verso opposto, ossia per inviduare le componenti armoniche, a partire dall'espressione della trasformata di Fourier. Nel caso di un coseno, che scriviamo

x$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ = Acos$$\left(\vphantom{ 2\pi f_{0}t+\varphi }\right.$$2$$\pi$$f₀t + $$\varphi$$ $$\left.\vphantom{ 2\pi f_{0}t+\varphi }\right)$$ = A$${\frac{\hbox {e}^{j\left( 2\pi f_{0}t+\varphi \right) }+\hbox {e}^{-j\left( 2\pi f_{0}t+\varphi \right) }}{2}}$$

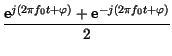
la $\mathcal {F}$-trasformata risulta:

X$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$	=	$$\mathcal {F}$$$$\left\{\vphantom{ \frac{A}{2}\left( \hbox {e}^{j2\pi ft}\hbox {e}^{j\varphi }+\hbox {e}^{-j2\pi ft}\hbox {e}^{-j\varphi }\right) }\right.$$$${\frac{A}{2}}$$$$\left(\vphantom{ \hbox {e}^{j2\pi ft}\hbox {e}^{j\varphi }+\hbox {e}^{-j2\pi ft}\hbox {e}^{-j\varphi }}\right.$$ej2$\pi$ftej$\varphi$ + e-j2$\pi$fte-j$\varphi$$$\left.\vphantom{ \hbox {e}^{j2\pi ft}\hbox {e}^{j\varphi }+\hbox {e}^{-j2\pi ft}\hbox {e}^{-j\varphi }}\right)$$ $$\left.\vphantom{ \frac{A}{2}\left( \hbox {e}^{j2\pi ft}\hbox {e}^{j\varphi }+\hbox {e}^{-j2\pi ft}\hbox {e}^{-j\varphi }\right) }\right\}$$
	=	$${\frac{A}{2}}$$$$\left\{\vphantom{ \hbox {e}^{j\varphi }\delta \left( f-f_{0}\right) +\hbox {e}^{-j\varphi }\delta \left( f+f_{0}\right) }\right.$$ej$\varphi$$$\delta$$$$\left(\vphantom{ f-f_{0}}\right.$$f - f0$$\left.\vphantom{ f-f_{0}}\right)$$ + e-j$\varphi$$$\delta$$$$\left(\vphantom{ f+f_{0}}\right.$$f + f0$$\left.\vphantom{ f+f_{0}}\right)$$ $$\left.\vphantom{ \hbox {e}^{j\varphi }\delta \left( f-f_{0}\right) +\hbox {e}^{-j\varphi }\delta \left( f+f_{0}\right) }\right\}$$

in cui riconosciamo

X₁ = ${\frac{A}{2}}$e^j$\varphi$ e X_-1 = ${\frac{A}{2}}$e^-j$\varphi$

come mostrato in figura.

Potenza di un coseno

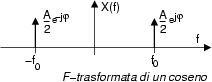
Cogliamo l'occasione per calcolare la potenza di una sinusoide. Applicando il teorema di Parseval si ottiene:

$\mathcal {P}$_x = $\left\vert\vphantom{ X_{1}}\right.$X₁$\left.\vphantom{ X_{1}}\right\vert^{2}_{}$ + $\left\vert\vphantom{ X_{2}}\right.$X₂$\left.\vphantom{ X_{2}}\right\vert^{2}_{}$ = 2${\frac{A^{2}}{4}}$ = ${\frac{A^{2}}{2}}$